Большинство физических величин определяется косвенными путями. Сначала производится непосредственное измерение одной или нескольких физических величин, количественно связанных с определяемой, а затем, с помощью соответствующих формул вычисляется значение определяемой величины. Очевидно, при этом ошибка вычисления определяемой величины зависит от величины погрешностей непосредственных измерений исходных величин.
Абсолютная ошибка функции одного переменного равна абсолютной ошибке аргумента, умноженной на первую производную этой функции.
 . (8)
. (8)
Относительная погрешность получится, если мы обе части равенства разделим на значение определяемой величины y:
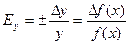 . (9)
. (9)
Как видно, в правой части равенства стоит дифференциал от натурального логарифма функции f(x), следовательно,
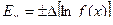 . (10)
. (10)
Относительная ошибка вычисления функции одного переменного равна дифференциалу натурального логарифма этой функции.
В качестве примера вычислим ошибку в определении объема шара по измеренному радиусу. Пусть радиус шара:
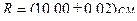 ;
;
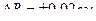 ;
; 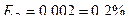 .
.
Объем шара подсчитывается по формуле:
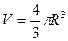 .
.
Тогда, абсолютная ошибка вычисления объема шара:
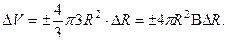
Подставим численные значения:
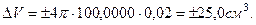
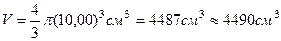 или
или 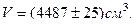
Относительная ошибка:
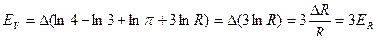 ,
,
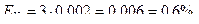
Если измеряемая величина является функцией нескольких непосредственно измеренных величин:
 .
.
Предельная абсолютная ошибка функции нескольких переменных равна сумме модулей произведений частных производных этой функции на соответствующие абсолютные ошибки.
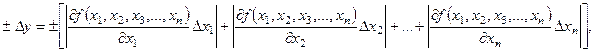 (11)
(11)
где частные производные 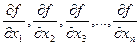 вычисляются как для обычной функции одной переменной (соответственно
вычисляются как для обычной функции одной переменной (соответственно  в предположении, что все остальные аргументы принимают постоянные значения.
в предположении, что все остальные аргументы принимают постоянные значения.
Предельная относительная ошибка функции нескольких переменных равна дифференциалу натурального логарифма этой функции, причем берется сумма абсолютных значений всех членов этого выражения.
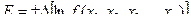 (12)
(12)
Пример:
Положим, объем параллелепипеда определяется по данным измерений его рёбер 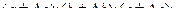
V = abc.
Для расчета предельной ошибки вычисления объема найдем частные производные от V по a,b и c:

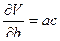 ;
; 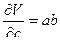
и выражение для абсолютной погрешности:
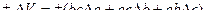 .
.
Для расчета относительной погрешности прологарифмируем V:
ln V = ln a + ln b + ln c.
Почленно дифференцируя и, переходя от дифференциалов к ошибкам, получим:
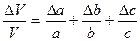 .
.
 2020-10-10
2020-10-10 250
250








