Комплексное число 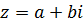 можно изобразить точкой плоскости с координатами (a; b). Плоскость xOy, на которой изображаются комплексные числа, называется комплексной плоскостью (рис 1.). При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют мнимой осью.
можно изобразить точкой плоскости с координатами (a; b). Плоскость xOy, на которой изображаются комплексные числа, называется комплексной плоскостью (рис 1.). При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют мнимой осью.
 у
у
M(a;b)


 b
b 
 О a х
О a х
Любое комплексное число 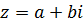 единственным способом определяется его действительной и мнимой частями. Каждому комплексному числу
единственным способом определяется его действительной и мнимой частями. Каждому комплексному числу 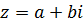 в комплексной плоскости соответствует единственная точка М(a; b), и, обратно, каждой точке (a; b) плоскости xOy соответствует единственное комплексное число. Например, число
в комплексной плоскости соответствует единственная точка М(a; b), и, обратно, каждой точке (a; b) плоскости xOy соответствует единственное комплексное число. Например, число  изображается точкой М(3;2). Сопряжённые числа расположены симметрично относительно действительной оси.
изображается точкой М(3;2). Сопряжённые числа расположены симметрично относительно действительной оси.
Комплексное число 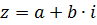 можно геометрически изобразить в виде вектора
можно геометрически изобразить в виде вектора 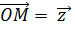 с началом в точке О(0;0) и концом в точке М(a; b).
с началом в точке О(0;0) и концом в точке М(a; b).
Модулем комплексного числа 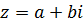 называется действительное число
называется действительное число 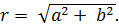 Модуль комплексного числа называется также абсолютной величиной этого числа.
Модуль комплексного числа называется также абсолютной величиной этого числа.
Пример.
Найти модули комплексных чисел 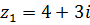 и
и 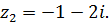
Решение:
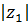 =
=  =
= 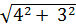 =
=  =
=  = 5;
= 5;
 =
= 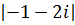 =
= 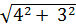 =
=  =
=  .
.
Из геометрической интерпретации комплексных чисел вытекают следующие свойства:
I. Длина вектора  равна
равна  .
.
II. Точки  и
и  симметричны относительно действительной оси.
симметричны относительно действительной оси.
III. Точки z и -z симметричны относительно точки О.
IV. Число  геометрически изображается вектором, построенным по правилу сложения векторов (правилу параллелограмма), соответствующих точкам
геометрически изображается вектором, построенным по правилу сложения векторов (правилу параллелограмма), соответствующих точкам  (рис.2).
(рис.2).
V. Расстояние между точками  и равно
и равно  .
.
 у
у




О х
Арифметические действия над комплексными числами.
1.  +
+ 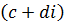 =
=  +
+ 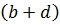
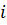 .
.
2.  –
– 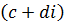 =
= 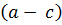 +
+ 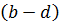
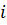 .
.
3. 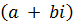 •
• 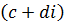 = ac + bci + adi – bd =
= ac + bci + adi – bd =  .
.
4. 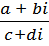 =
= 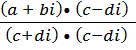 =
= 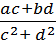 +
+ 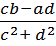 i, c + di ≠ 0.
i, c + di ≠ 0.
 2020-10-10
2020-10-10 297
297








