Группы ВРБ, ВЭБ, КРБ2_20. 1 неделя, лекция, практика

Занятие по дисциплине: «Математический анализ», лекция,  практика.

Тема: Теория пределов.

Теория.

Пусть имеется функция   f(x). При этом, если при стремлении аргумента функции x к некоторому своему значению x₀ (т.е. значение аргумента бесконечно приближается к   x₀, но не становится ему равным), сама функция стремится к некоторому своему значению А, то это значение называется пределом функции  f(x)  при x стремящемся к x₀. Это обозначается так:

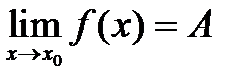, где lim - обозначение предела.

Замечание.

Определение справедливо и для случая, когда аргумент x стремится к +∞ или -∞.

Таким образом, во многих случаях для нахождения предела достаточно в выражение функции подставить предельное значение аргумента. При этом, если получится вполне конкретный результат, то он и будет являться пределом функции. Например:

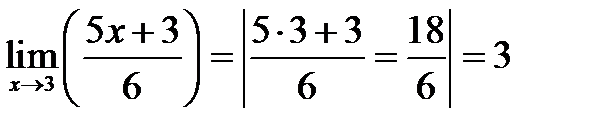
Подстановка предельного значения производится в промежуточном действии, которое выделено вертикальными линиями.

Однако, во многих случаях подстановка предельного значения не приводит к конкретному результату: результат получается не поддающимся оценке. Такие результаты называются неопределенностями. Существует четыре вида неопределенностей.

1.

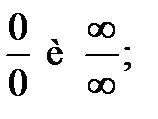
2.

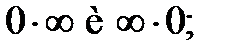
3.

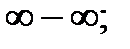
4.

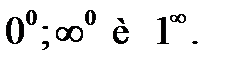
Хотя эти результаты и не поддаются оценке, но не означают отсутствие предела. В этом случае для его нахождения неопределенность необходимо «раскрыть». Раскрытию неопределенностей и посвящена основная часть теории пределов.

Замечание.

Следует отметить. Что следующие выражения не являются неопределенностями и дают конкретный результат:

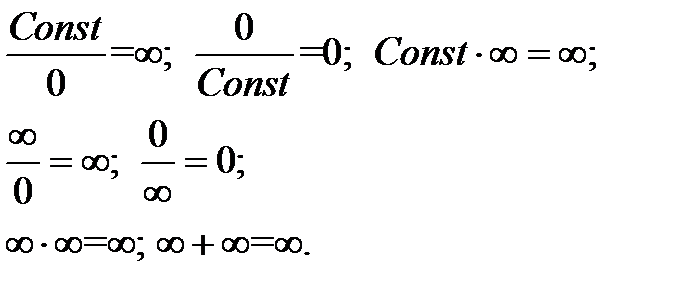
Некоторые способы раскрытия неопределенностей.

Решение любого предела следует начинать с промежуточного действия, заключающегося в подстановке в функцию предельного значения аргумента. При этом, если получен результат, отличающийся от неопределенности, то он и будет ответом.

1. Пусть функция представляет собой отношение двух многочленов P_m(x) и Q_n(x), где m и n соответственно старшие степени х этих многочленов, а   х→∞. Подстановка при этом дает неопределенность 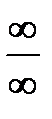 . Она раскрывается по следующему правилу:

.

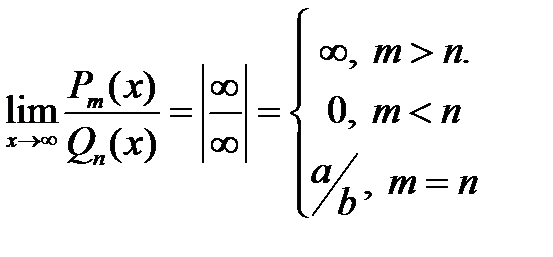Таким образом, предел равен ∞, если больше старая степень числителя; 0, если больше старая степень знаменателя и отношению коэффициентов а и b при старших степенях, если эти степени равны.

Примеры.

1.

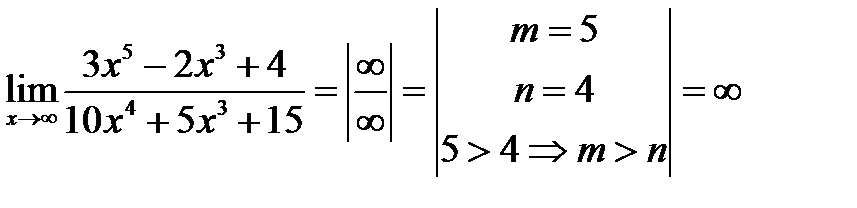
2.

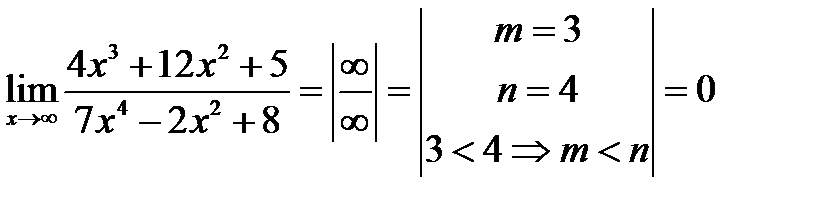
3.

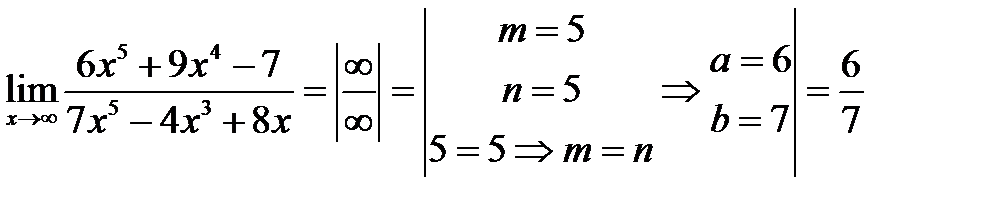
4.

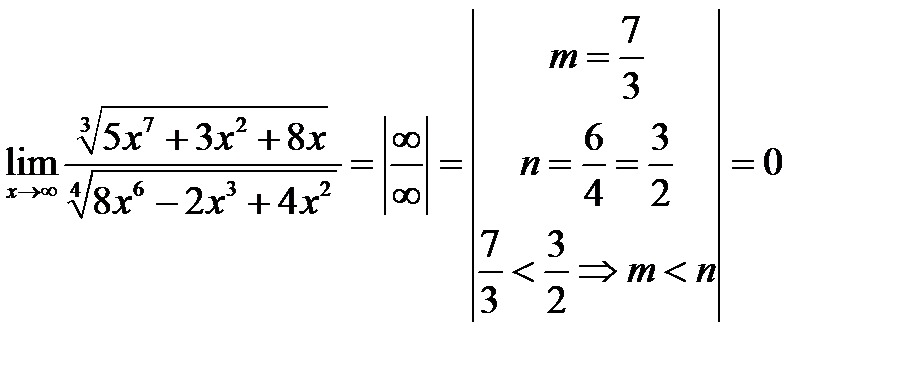
5.

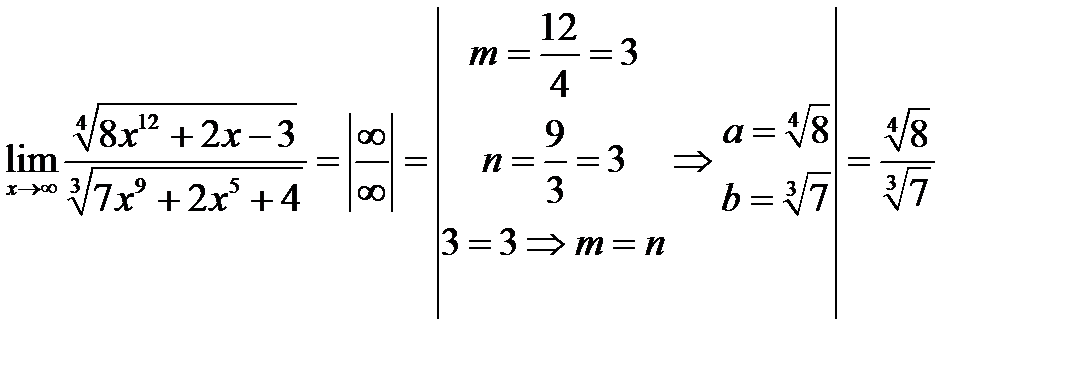
Замечание.

Рассмотренное правило работает только при х→∞.

2. Пусть функция представляет собой отношение двух многочленов P(x) и Q(x), а х→а, где а – const. Подстановка при этом дает неопределенность 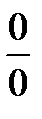 . в этом случае в числителе и знаменателе выделяется множитель (х-а), и дробь сокращается на этот множитель.

Замечание.

При выделении множителей очень часто используются формулы сокращенного умножения и формула разложения квадратного трехчлена на множители.

Формулы сокращенного умножения:

1.

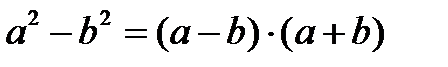
2.

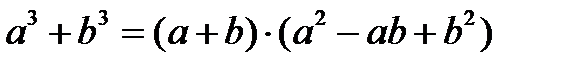
3.

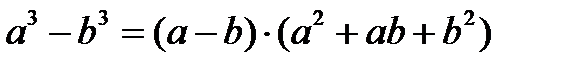
4.

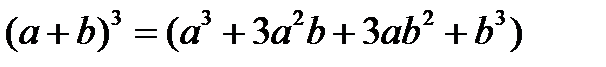
5.

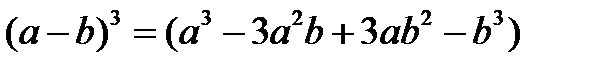
Формула разложения квадратного трехчлена на множители:

6. ,

 где х₁ и х₂ корни соответствующего квадратного уравнения, которые находятся пол формуле:

 

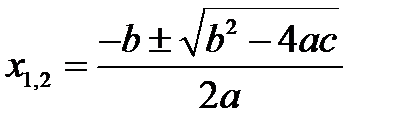или по теореме Виетта.

 

Примеры.

1.

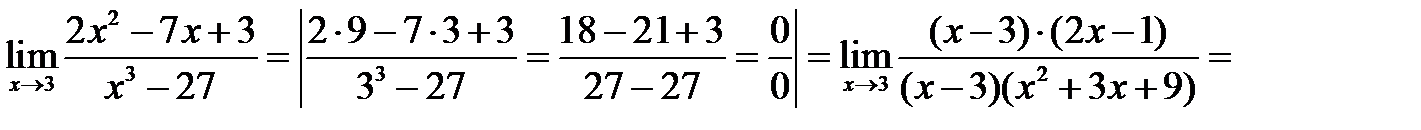
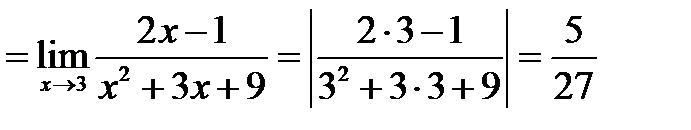
Корни числителя: ,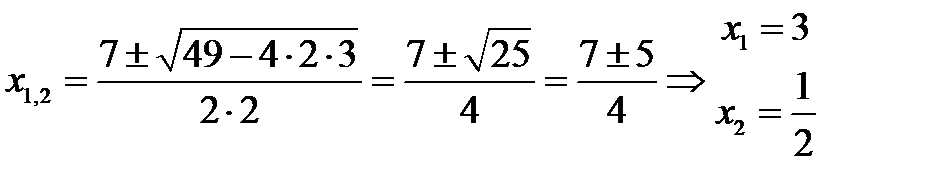

Тогда  по формуле 6: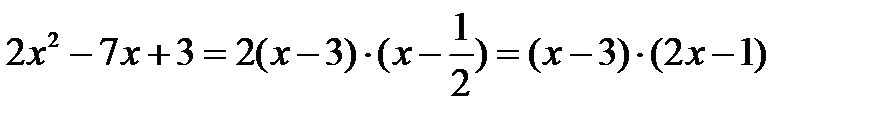

Знаменатель раскладывается по формуле 3: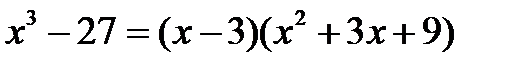

2.

Числитель раскладывается по формуле 1: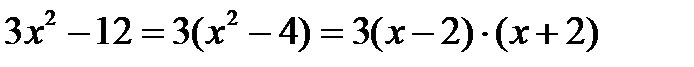

Корни знаменателя: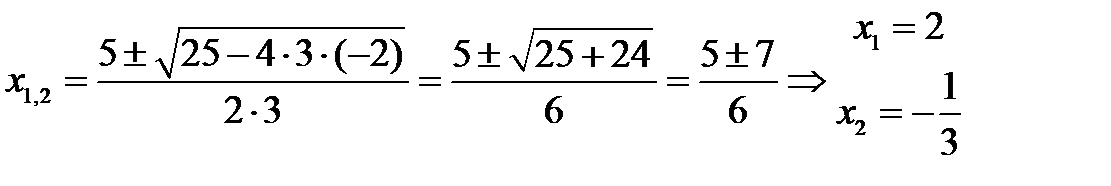

Тогда по формуле 6: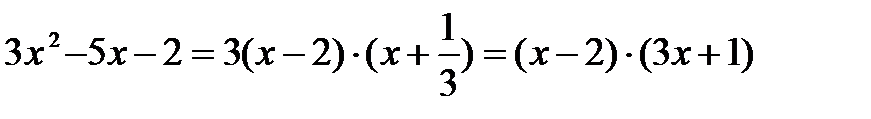

3.

 

Корни числителя: ,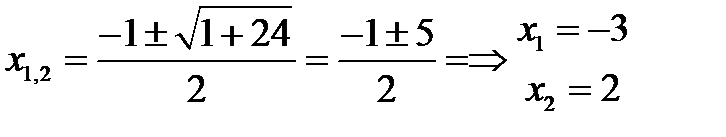

Тогда по формуле 6: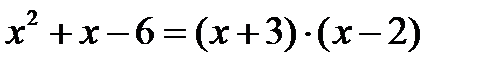

Корни знаменателя: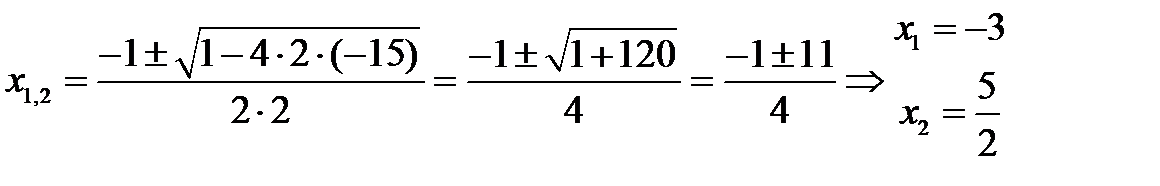

Тогда по формуле 6: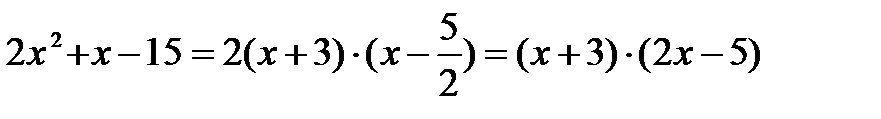

3. Если функция представляет собой разность f(x)= f₁(x)- f₂(x) и подстановка предельного значения дает неопределенность вида ∞-∞, то выражение можно привести к неопределенностям, рассмотренным выше в 1 и 2, путем приведения выражения к общему знаменателю.

Примеры.

1.

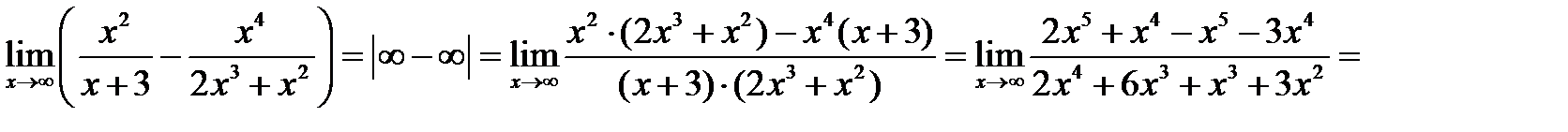
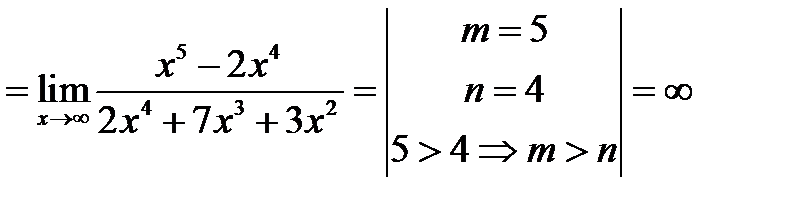
2.

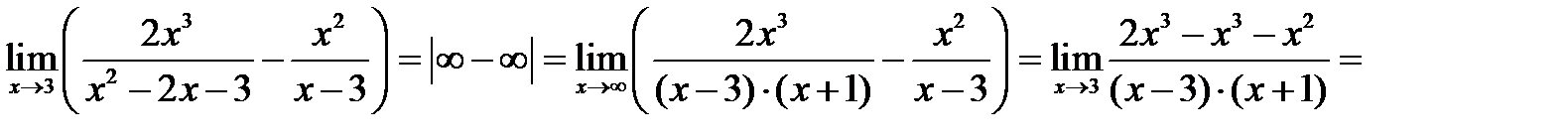
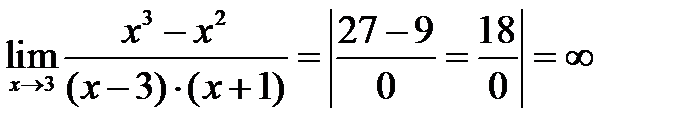
Замечание к примеру 2. Знаменатель первой дроби разложен на множители по формуле 6.

 

4. Если функция содержит квадратные или кубические корни, то часто выражение может быть преобразовано по формулам сокращенного умножения (формулы 1, 2, 3), что позволяет уйти от неопределенностей.

Примеры.

1.

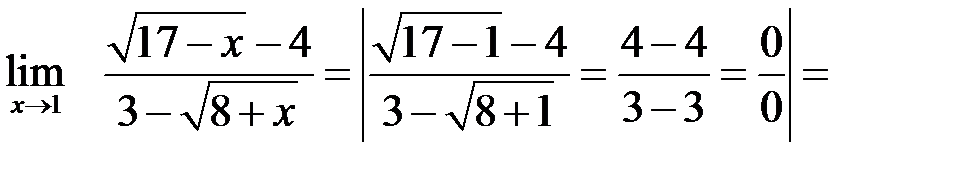
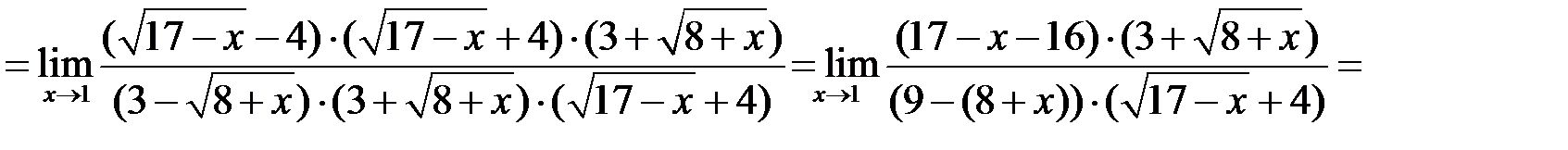
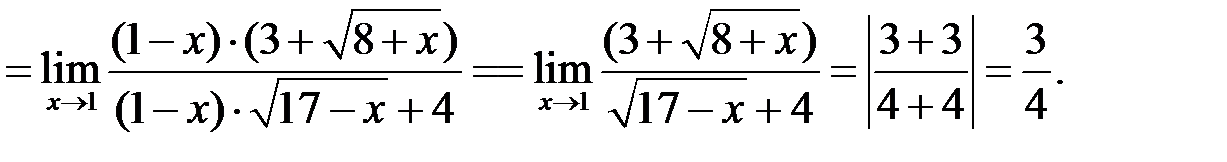
Замечание к примеру 1. И числитель и знаменатель преобразованы по формуле сокращенного умножения 1 путем выделения разности квадратов. Для этого всю дробь домножили на сопряженные числителю и знаменателю выражения. А затем свернули по формуле.

Числитель: 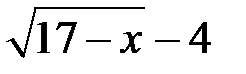. Сопряженное ему выражение 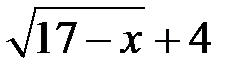, отличается лишь знаком между корнем и константой. Домножать на сопряженное выражение надо и числитель и знаменатель.

Аналогично поступили с выражением знаменателя.

Произведение двух сопряженных выражений сворачивается по формуле разности квадратов:

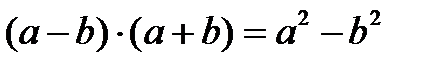
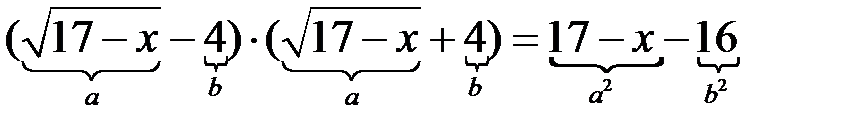
Со знаменателем аналогично.

2.

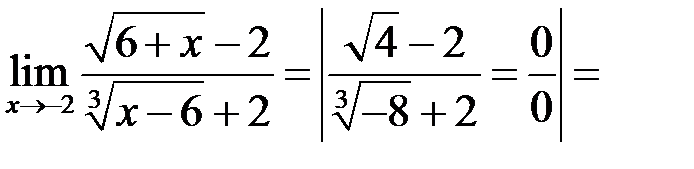
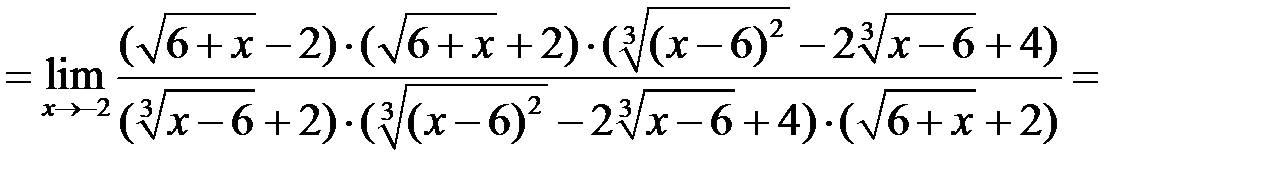
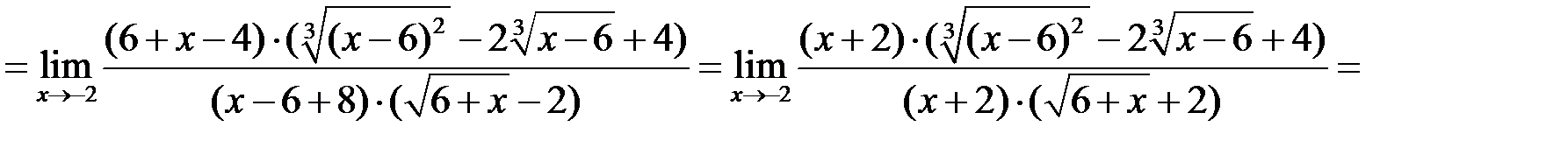
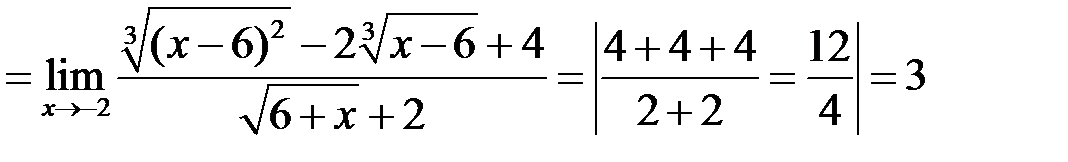
Замечание к примеру 2. Числитель преобразовали так же, как в примере 1. Знаменатель преобразованы по формуле сокращенного умножения 2 путем выделения суммы кубов. Для этого всю числитель и знаменатель дроби домножили на неполный квадрат суммы, а затем свернули по формуле (2).

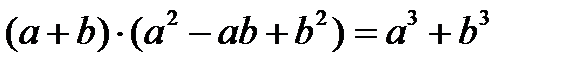
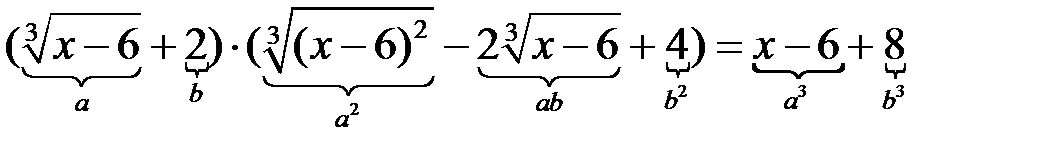
5. Если функция, дающая при подстановке предельного значения неопределенность, содержит корни разных порядков из одного и того же выражения, то в целом ряде случае исходное выражение целесообразно преобразовать через введение новой переменной в степени, позволяющей избавиться от всех корней.

Пример.

 

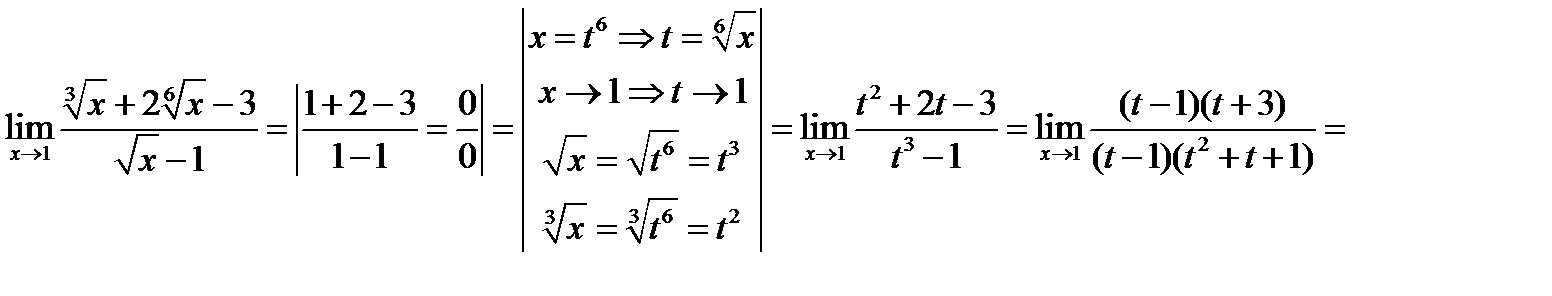
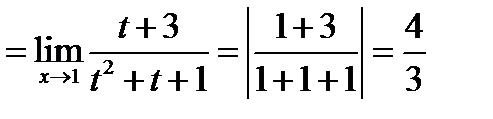
Практика.

Решить самостоятельно на занятии:

Б.П.Демидович Задачи и упражнения по математическому анализу. №183,184,185,186,188,189; 192,193.194; 203,205,206,207; 199,200

В задачнике Демидовича Б.П. есть краткая теория и разобранные примеры. Ответы в конце задачника.

 

Дома:

Г.Н.Берман Сборник задач по курсу математического анализа №268,271,281,282,283,272,275,277,286,293,295,297. Ответы в конце задачника.

 

Отчет о проделанной домашней работе высылать в виде фото или скана страниц тетради. Фото должны быть четкими и сориентированы для удобного чтения. Перед решением указать ФИО и дату выполнения задания. Высылать фото или скан страниц тетради с работой мне на адрес: silin58@rsatu.ru