Алгоритм решения дифференциального уравнения первого порядка

ПРАКТИЧЕСКАЯ РАБОТА №6

 

Тема: Решение дифференциальных уравнений первого порядка с разделяющимися переменными.

Цель работы: Закрепить и систематизировать знания по теме «Обыкновенные дифференциальные уравнения».

Задание: Проверить подстановкой, что данная функция является общим решением (интегралом) данного дифференциального уравнения:

1.	1. 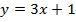;	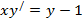4.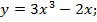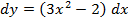
2.	1.	5.	;
3.	1.    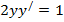     ;	6.	;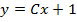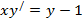

Задание: Найти общие решения дифференциальных уравнений методом разделения переменных:

7.		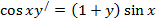10.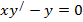
8.		11.
9.		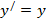12.

Задание: Найти частные решения уравнений первого порядка, удовлетворяющие указанным начальным условиям:

13.		16.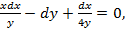
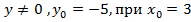
14.		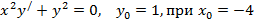17.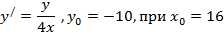
15.		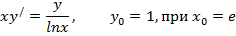18.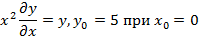

Задание: Решить линейные уравнения первого порядка:

19.		22.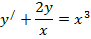
20.		23.
21.		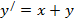24.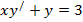

Задание: Найти частные решения однородных дифференциальных уравнений:

25.	применение дифференциальных уравнений при решении задач задача 2.126 уч-к Омельченко «Математика»	28.	применение дифференциальных уравнений при решении задач задача 2.129 уч-к Омельченко «Математика»
26.	применение дифференциальных уравнений при решении задач задача 2.127 уч-к Омельченко «Математика»	29.	применение дифференциальных уравнений при решении задач задача 2.126 уч-к О
27.	применение дифференциальных уравнений при решении задач задача 2.128 уч-к Омельченко «Математика»	30.	применение дифференциальных уравнений при решении задач задача 2.127 уч-к Омельченко «Математика»

Пояснения к работе:

Необходимые формулы:

Алгоритм решения дифференциального уравнения первого порядка

y' = f(x,y) с разделяющими переменными

1. Рассмотрим производную y' как отношение дифференциалов ,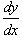

2. Перенесем dx в правую часть и разделим уравнение на h(y):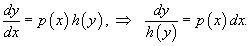

3. Разделим обе части уравнения на h(y) ≠ 0

4. Запишем уравнение в форме:

5. Проинтегрируем дифференциальное уравнение:

где C − постоянная интегрирования.

6. Вычислим интегралы, получаем выражение

 

Алгоритм решения дифференциального уравнения первого порядка

вида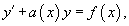

1. Пусть y = uv, тогда по правилу дифференцирования произведения функций 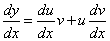и линейное дифференциальное уравнения первого порядка примет вид  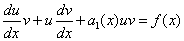или

2. Выберем функцию v(x) так, чтобы в этом уравнении выражение в скобках обратилось в нуль: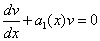

3. Разделим в уравнении 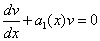  переменные.

4.  Выполним почленное интегрирование, найдём функцию v. Так как функция v - решение уравнения, то её подстановка в уравнение  даёт

5. Найдём функцию u как общее решение этого уравнения.

6. Найдем решение исходного линейного дифференциального уравнения первого порядка. Оно равно произведению функций y = uv.

Содержание отчета

1. Титульный лист в соответствии с СТП1.2-2005.

2. Цель работы

3. Задание

4. Выполненная практическая работа в соответствии с заданием

5. Ответы на контрольные вопросы

6. Вывод

Контрольные вопросы:

1. Дайте определение дифференциального уравнения.

2. Дайте определение общего решения дифференциального уравнения.

3. Дайте определение дифференциального уравнения с разделяющими переменными.

4. Дайте определение дифференциального уравнения первого порядка.

5. Запишите формулу уравнение Бернулли.