Практическая работа № 7
Тема занятия: Решение задач по теме «Линии 2-го порядка»
Цель: закрепить и систематизировать теоретические знания,
научиться решать задачи по теме «Линии 2-го порядка».
План выполнения практической работы
1. Изучение методических рекомендаций по решению задач и выполнение упражнений и задач.
2. Выполнение практической самостоятельной работы по вариантам.
3. Письменные ответы на контрольные вопросы
Задания для практической работы.
Методические рекомендации по решению упражнений и задач.
1.Окружность и её уравнение.
Каноническое уравнение окружности имеет вид:
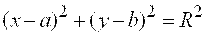 , (1)
Где(a, b)– координаты центра, а R – радиус окружности.
2. Эллипс и его уравнение.
Каноническое уравнение эллипса: , (1)
Где(a, b)– координаты центра, а R – радиус окружности.
2. Эллипс и его уравнение.
Каноническое уравнение эллипса:
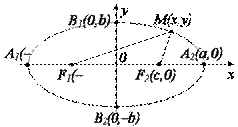 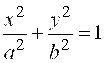 , (2)
Где а – большая полуось, в – малая полуось, , (2)
Где а – большая полуось, в – малая полуось,
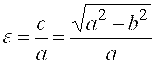 – эксцентриситет эллипса.
Прямую, на которой расположены фокусы эллипса F1 u F2, называют фокальной осью, а – эксцентриситет эллипса.
Прямую, на которой расположены фокусы эллипса F1 u F2, называют фокальной осью, а
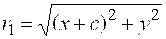 и и 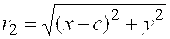 – фокальными радиусами.
Прямые x= – фокальными радиусами.
Прямые x= 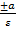 называют директрисами эллипса.
Пример 1. Доказать, что уравнение называют директрисами эллипса.
Пример 1. Доказать, что уравнение
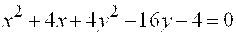 определяет эллипс. Найти координаты его центра симметрии.
Решение. Преобразуем данное уравнение, выделив полные квадраты по
определяет эллипс. Найти координаты его центра симметрии.
Решение. Преобразуем данное уравнение, выделив полные квадраты по 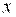 и по и по 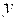 : :
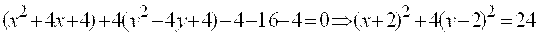 .
Обозначим .
Обозначим 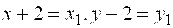 , где , где 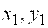 – новые переменные. Тогда уравнение примет вид – новые переменные. Тогда уравнение примет вид  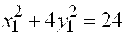 или, приводя к каноническому виду, или, приводя к каноническому виду, 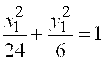 .
Сравнивая полученное уравнение с уравнением (2) убеждаемся, что кривая – эллипс. Центр его симметрии находится в точке (-2;2).
3. Гипербола и её уравнение.
Каноническое уравнение гиперболы: .
Сравнивая полученное уравнение с уравнением (2) убеждаемся, что кривая – эллипс. Центр его симметрии находится в точке (-2;2).
3. Гипербола и её уравнение.
Каноническое уравнение гиперболы:
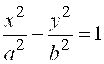 , (3)
Где , (3)
Где 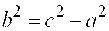 .
Точки .
Точки 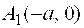 , , 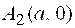 называются вершинами гиперболы, прямые называются вершинами гиперболы, прямые 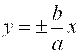 являются асимптотами гиперболы, являются асимптотами гиперболы, 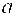 – действительная полуось, – действительная полуось, 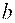 – мнимая полуось, – мнимая полуось, 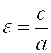 – эксцентриситет гиперболы, прямые – эксцентриситет гиперболы, прямые 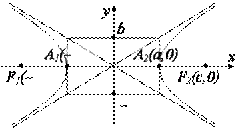 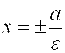 – ее директрисы.
Пример 2. Написать уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в точках – ее директрисы.
Пример 2. Написать уравнение гиперболы и ее асимптот, если фокусы гиперболы находятся в точках 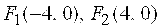 и длина вещественной оси равна 6.
Решение. По условию и длина вещественной оси равна 6.
Решение. По условию 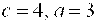 , тогда из формулы , тогда из формулы 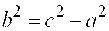 найдем найдем 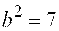 . Каноническое уравнение гиперболы: . Каноническое уравнение гиперболы:  уравнения асимптот: уравнения асимптот: 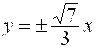 .
Пример 3. Написать уравнение гиперболы, проходящей через точку .
Пример 3. Написать уравнение гиперболы, проходящей через точку 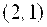 , асимптоты которой , асимптоты которой 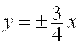 .
Решение. Из уравнения асимптот следует, что .
Решение. Из уравнения асимптот следует, что 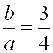 . Уравнение гиперболы будем искать в виде . Уравнение гиперболы будем искать в виде 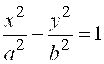 . Так как точка . Так как точка 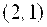 лежит на гиперболе, то лежит на гиперболе, то  . Решая систему . Решая систему  найдем найдем 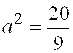 , , 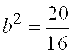 . Получаем . Получаем 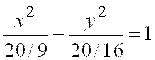 или или 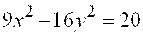 .
4. Парабола и её уравнение.
Каноническое уравнение параболы .
4. Парабола и её уравнение.
Каноническое уравнение параболы
 , (4)
Где , (4)
Где 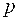 (параметр параболы) – расстояние между фокусом и директрисой, а уравнение ее директрисы (параметр параболы) – расстояние между фокусом и директрисой, а уравнение ее директрисы 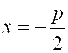 .
Так как уравнение параболы содержит .
Так как уравнение параболы содержит 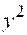 , то она симметрична относительно оси , то она симметрична относительно оси 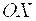 . Ось симметрии параболы называется осью параболы.
Вершиной параболы называется точка пересечения параболы с ее осью симметрии. . Ось симметрии параболы называется осью параболы.
Вершиной параболы называется точка пересечения параболы с ее осью симметрии.
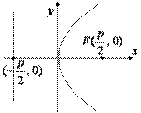 Пример 4. Парабола с вершиной в начале координат проходит через точку Пример 4. Парабола с вершиной в начале координат проходит через точку 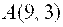 и симметрична относительно оси и симметрична относительно оси 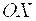 . Написать ее каноническое уравнение.
Решение. Подставляя координаты точки . Написать ее каноническое уравнение.
Решение. Подставляя координаты точки 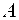 в уравнение (22), найдем, что в уравнение (22), найдем, что 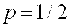 . Значит, уравнение параболы . Значит, уравнение параболы 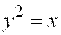 .
Пример 5. Доказать, что уравнение .
Пример 5. Доказать, что уравнение 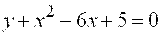 определяет параболу. Найти значение ее параметра и координаты вершины.
Решение. Выделяя полный квадрат, получим определяет параболу. Найти значение ее параметра и координаты вершины.
Решение. Выделяя полный квадрат, получим 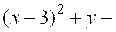 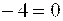 . Если положить . Если положить 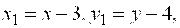 то уравнение примет вид то уравнение примет вид  . Сравнивая его с каноническим уравнением (22), находим . Сравнивая его с каноническим уравнением (22), находим 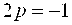 , откуда , откуда 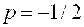 . Вершина параболы находится в точке . Вершина параболы находится в точке 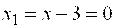 , , 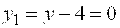 , то есть , то есть 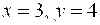 .
2. Самостоятельная работа.
Вариант I.
1. Найдите координаты центра и радиус окружности: .
2. Самостоятельная работа.
Вариант I.
1. Найдите координаты центра и радиус окружности:
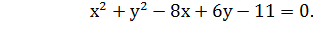 2. Найдите эксцентриситет эллипс:
2. Найдите эксцентриситет эллипс: 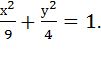 Вариант II.
1.Найдите уравнения асимптот и изобразите схематично гиперболу:
Вариант II.
1.Найдите уравнения асимптот и изобразите схематично гиперболу:
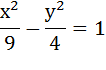 2. Запишите уравнение директрисы параболы и постройте её схематично:
У2 =-12х.
2. Запишите уравнение директрисы параболы и постройте её схематично:
У2 =-12х.
|
 2020-10-11
2020-10-11 135
135







