2020-10-12
162Тема: График и свойства функций sin.
Синус (sin) — название тригонометрической функции, появившееся благодаря удивительной цепочке искажений во время переводов математических трактатов. Древние индийские математики называли функцию «полу-тетивой», а затем просто «тетивой» — «джива», так как при геометрическом построении изображение напоминало лук. Арабские математики при знакомстве с трудами индийских коллег не стали переводить слово «джива» на арабский, а просто записали его по буквам. В процессе адаптации, устного использования и пр. оно превратилось в арабское выражение «джайб», которое можно перевести как пазуха, складка, карман, впадина. Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos.
y = sin x
а) Область определения: D (sin x) = R.
б) Множество значений: E (sin x) = [ – 1, 1 ].
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = 2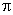 
.
д) Нули функции: sin x = 0 при x = 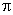n, n 
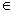Z.
е) Промежутки знакопостоянства:
; 
.
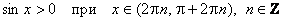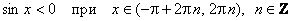ж) Промежутки монотонности:
;
.
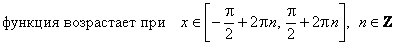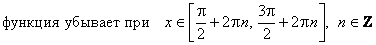з) Экстремумы:
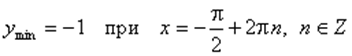
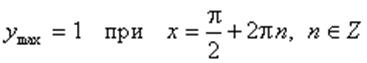
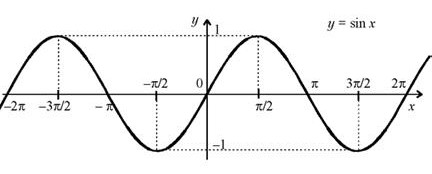
График функции y = sin x изображен на рисунке.
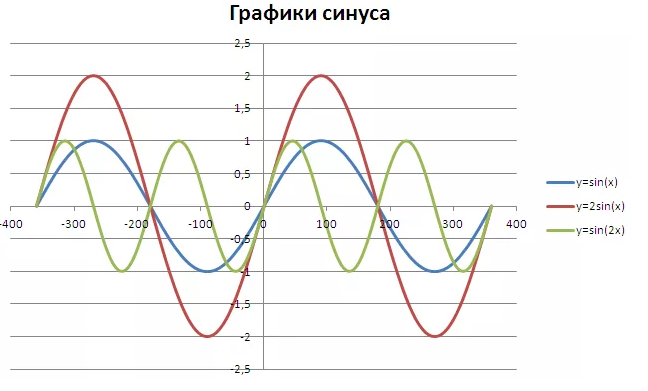
Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом.
Пример 1. Найдем все корни уравнения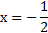 
, принадлежащие отрезку 
.
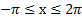Построим графики функци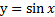й 
и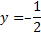 
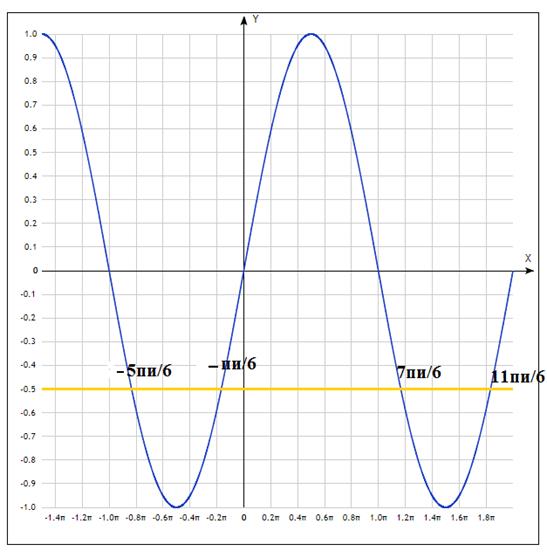
Рис. – графики функци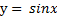й 
и .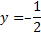
Графики пересекаются в четырёх точках, абсциссы которых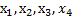 
являются корнями уравнения 
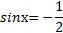. На выбранном отрезке от 
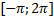корни уравнения симметричны: 
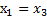и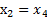 
. Из рисунка видно, что симметричность корней объясняется периодичностью функции: 
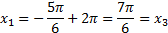аналогично для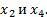 
Ответ: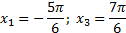 
; 
.
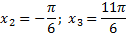Пример 2. Найти все решения неравенства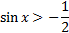 
, принадлежащие отрезку .
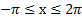Из рисунка видно, что график функции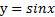 
лежит выше графика функции 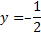на промежутках 
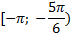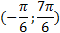и 
и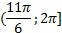 
Ответ: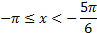 
, 
, 
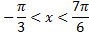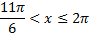
Домашнее задание:
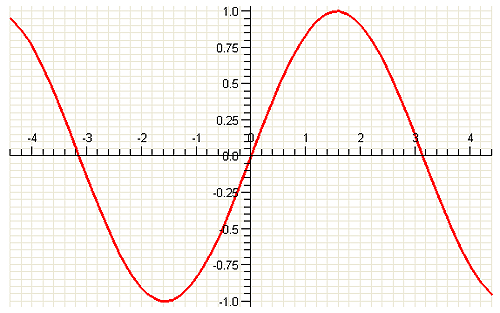
1.По графику функции у = sin x определить: a) sin 2; б) sin 4; в) sin (—3).
2.По графику функции у = sin x определить, какое число из интервала
[ — π/ 2, π/ 2 ] имеет синус, равный: а) 0,6; б) —0,8.
3. По графику функции у = sin x определить, какие числа имеют синус,
равный 1/2.
4. Найти приближенно (без использования таблиц): a) sin 1°; б) sin 0,03;
в) sin (—0,015); г) sin (—2°30').
