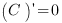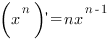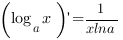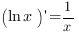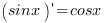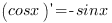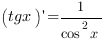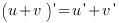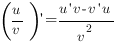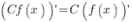Вставьте пропущенные слова

Повторение

Производная

Предел разностного отношения_{---------------------------------------------------------------------------} называется

производной функции и обозначается _{------------------------------------------------}

Операция нахождения производной функции называется _{------------------------------------------------------------------} В результате выполнения этой операции мы по определенным правилам получаем другую функцию:

Заполните таблицу

Свойства производной	Написать формулу	Приведи пример Реши пример
Производная константы		8 \ =
		(0,75)\ =
		(1/2)\ =
Производная степенной функции
Производная показательной функции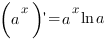
Производная логарифма:
Производные тригонометрических функций:
Правила дифференцирования: 1 Производная суммы двух функций		(Х5  + Х8)/
		(sin x +cosx) /
		(Lg x + cos x)\
2.Производная произведения двух функций:		(Х5  * Х8)/
		(sin x *cosx)|
		(Lg x * cos x)\
3. Производная дроби:
		(sin x: cosx)|
		(Lg x  : cos x)\
/4.Производная произведения функции на число		(3Х5)/
		(4Х3)/
Вычисли производную

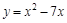
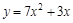
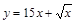
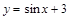
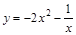
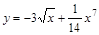
Ответе на вопросы:

1.В чём заключается геометрический смысл производной?

2.В чём заключается механический смысл производной?

3.Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?

4.Согласны ли вы с утверждением? Обоснуйте свой ответ

• С¹ = 0------------------------------------------

• Х¹ =1 ------------------------------------------

• (Х ^п)¹ = Х ^{п + 1} ------------------------------------------------------------------------------------------------

• (Sin x)¹ = Cos x ---------------------------------------------------------------------------------------------

• (f(x):g(x))¹  = f ¹(x):g¹(x) ----------------------------------------------------------------------------------

• К = Cos a = f¹ (х) --------------------------------------------------------------------------------------------

 

• На промежутке убывания функции её производная больше нуля.-----------------------

• Если производная функции в некоторой точке равна нулю, то в этой точке имеется экстремум! --------------------------------------------------------------------------------------

• Производная частного равна произведению производных.---------------------------------

-------------------------------------------------------------------------------------------------------------------

• Наибольшее и наименьшее значения функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка. ------------------------------------------------------------------------------------------------------------------------------------------

• Если функция отрицательна, то производная тоже отрицательна.------------------------------------------------------------------------------------------------------------------------------------------

 

5. Укажите правильный ответ.   

 При вычислении производной постоянный множитель можно:

 

1) возводить в квадрат;

2) выносить за знак производной;

3) не принимать во внимание;

4) принять за нуль;

 

   Точка, производная в которой равна 0 и меняет знак с «+» на «-»называется:

 

 1) точкой максимума;

 2) критической точкой;

 3) точкой перегиба;

 4) точкой минимума;

       

6. Допишите предложение:

 

1. Функцию, имеющую производную в точке называют _{------------------------------------------------------------------}

2. Если f^\ (x) <0 на некотором промежутке, то функция -------------------------------------

3. скорость прямолинейного движения равна _{--------------------------------------------------------------------------------}

4. Геометрический смысл производной состоит в том, что_{---------------------------------------------------------}

 

7.   Установите правильную последовательность.

Чтобы найти точки экстремума, надо:

1. найти критические точки;

2.  найти производную;

3. найти область определения функции;

4. выявить точки максимума и минимума;

5. определить знак производной в промежутках;

6. отметить критические точки на числовой прямой;

 

 

8.По знакам производной определите интервалы возрастания убывания функции. Дайте характеристику точек х = 1 и х = 5