Пусть ЛНЧ (линейная непрерывная часть) (рис. **) описывается дифференциальным уравнением в векторно-матричной форме
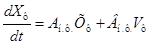 (*)
(*)
Общее решение данного дифференциального уравнения записывается в виде
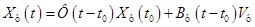 ,
,
где 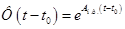 - фундаментальная (переходная) матрица состояния,
- фундаментальная (переходная) матрица состояния,
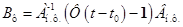 - матрица, учитывающая влияние внешних возмущений,
- матрица, учитывающая влияние внешних возмущений,
 - вектор состояния ЛНЧ.
- вектор состояния ЛНЧ.

Рассмотрим четыре случая работы мостового преобразователя.
1. Транзисторы 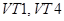 открыты, а транзисторы
открыты, а транзисторы  закрыты (рис. **). Интервал
закрыты (рис. **). Интервал  на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Источник тока
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Источник тока 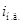 учитывает резкие изменения тока на выходе, например, сброс или наброс нагрузки. Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.
учитывает резкие изменения тока на выходе, например, сброс или наброс нагрузки. Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.


Приведем его к нормальной форме Коши. После несложных математических преобразований получим

где 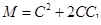 .
.
Введем следующий вектор состояния ЛНЧ 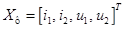 , где Т – знак транспонирования. Вектор внешних воздействий –
, где Т – знак транспонирования. Вектор внешних воздействий –  . Тогда матрицы
. Тогда матрицы  и
и 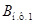 запишутся:
запишутся:
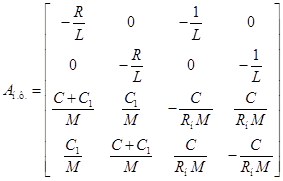
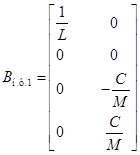
Решение векторно-матричного дифференциального уравнения (**) на интервале 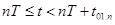 запишется в следующем виде:
запишется в следующем виде:
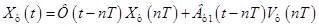 ,
,
где 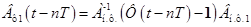 ,
,  - единичная матрица.
- единичная матрица.
Значение вектора состояния в конце интервала открытого состояния транзисторов 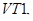
 , т.е. при
, т.е. при  определяется уравнением
определяется уравнением
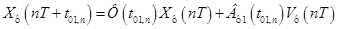 ,(**1)
,(**1)
где  .
.
2. Транзисторы 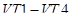 закрыты, ток протекает через диоды
закрыты, ток протекает через диоды 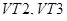 . Интервал времени
. Интервал времени 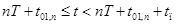 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).

Запишем систему уравнений по законам Кирхгофа
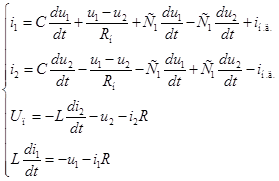
Приведем его к нормальной форме Коши. После несложных математических преобразований получим

Матрицы  и
и 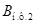 запишутся:
запишутся:
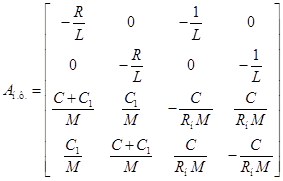

Решение векторно-матричного дифференциального уравнения (**) на интервале  запишется в следующем виде:
запишется в следующем виде:
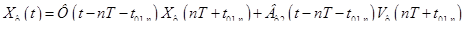 ,
,
где  .
.
Значение вектора состояния в момент времени  определяется уравнением
определяется уравнением
 ,(**2)
,(**2)
где 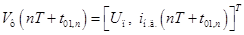 .
.
3. Транзисторы  открыты, а транзисторы
открыты, а транзисторы 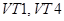 закрыты (рис. **). Интервал
закрыты (рис. **). Интервал  на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **). Для схемы запишем систему уравнений по первому и второму закону Кирхгофа.


Приведем его к нормальной форме Коши. После несложных математических преобразований получим
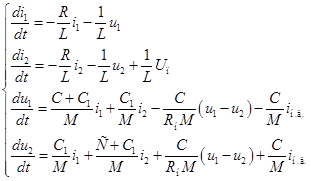
Матрицы  и
и 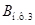 запишутся:
запишутся:
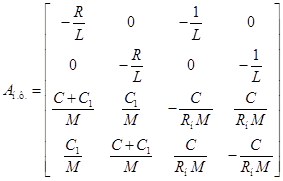
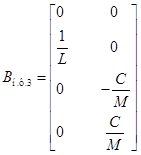
Решение векторно-матричного дифференциального уравнения (**) на интервале 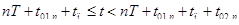 запишется в следующем виде:
запишется в следующем виде:
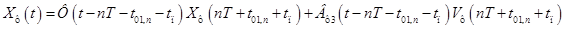 ,
,
где  .
.
Значение вектора состояния в момент времени 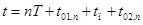 определяется уравнением
определяется уравнением
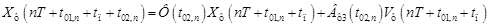 ,(**3)
,(**3)
где 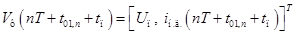 .
.
4. Транзисторы 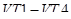 закрыты, ток протекает через диоды
закрыты, ток протекает через диоды 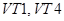 . Интервал времени
. Интервал времени 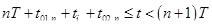 на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).
на рис. **. Схема замещения преобразователя в этом случае будет выглядеть следующим образом (рис. **).

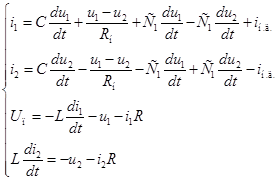
Приведем его к нормальной форме Коши. После несложных математических преобразований получим
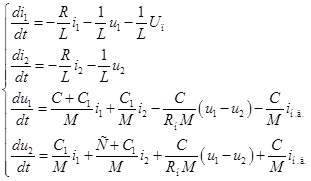
Матрицы  и
и 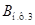 запишутся:
запишутся:
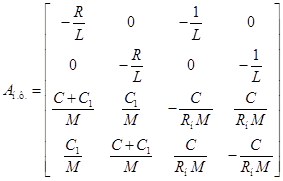
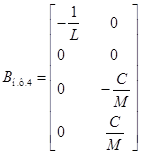
Решение векторно-матричного дифференциального уравнения (**) на интервале  запишется в следующем виде:
запишется в следующем виде:
 ,
,
где 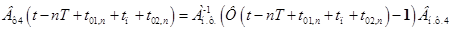 .
.
Значение вектора состояния в момент времени 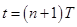 определяется уравнением
определяется уравнением
 ,(**4)
,(**4)
где 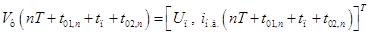 .
.
Для упрощения расчетов будем считать что напряжение питания  не меняется с течением времени, а изменение дополнительного тока нагрузки
не меняется с течением времени, а изменение дополнительного тока нагрузки 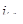 происходит в начале каждого интервала дискретизации. Тогда можно положить, что
происходит в начале каждого интервала дискретизации. Тогда можно положить, что 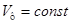 на интервале
на интервале 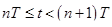 .
.
Используя уравнения (**1) – (**4) получим разностное уравнение ЛНЧ на интервале дискретизации. При преобразовании уравнения учтем, что 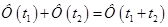 . В результате преобразования имеем:
. В результате преобразования имеем:
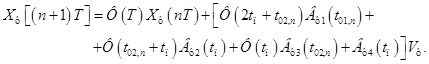
Чтобы найти решение этого уравнения необходимо найти длительности 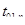 и
и 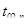 . При сигнале задания
. При сигнале задания 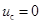
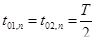
 2020-10-12
2020-10-12 253
253








