Мета роботи: дослідження законів коливального руху на прикладі фізичного маятника, визначення прискорення сили тяжіння.
Обладнання: фізичний маятник (однорідний сталевий стержень), лінійка, секундомір
Теоретичні відомості
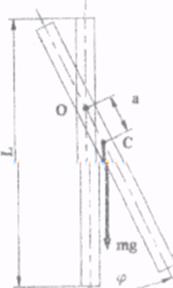
Фізичним маятником називається будь-яке тверде тіло, яке під дією сили тяжіння може вільно коливатись навколо нерухомої горизонтальної осі. У даній роботі фізичним маятником є однорідний сталевий стержень довжиною L.. На стержень нанесено шкалу і закріплено опорну призму, гостре ребро якої є віссю коливання маятника. Переміщуючи призму вздовж стержня, можна змінювати відстань від точки підвісу маятника О до його центру мас С (рис.2 1)*. * Можливі інші способи підвішування фізичного мастика, які лають можливість змінювати положення точки підвісу, а також такі, що забезпечують малий момент сил терта.
Будемо вважати, що моменти сил тертя та опору малі. У цьому випадку рух маятника визначається тільки моментом сили тяжіння
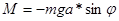
де а - відстань ОС від точки підвісу до центру мас,  - кут відхилення маятника від положення рівноваги. Застосовуючи основне рівняння динаміки обертального руху твердого тіла, отримаємо:
- кут відхилення маятника від положення рівноваги. Застосовуючи основне рівняння динаміки обертального руху твердого тіла, отримаємо:
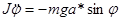 (2.1)
(2.1)
де J - момент інерції маятника відносно осі О; 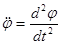 - кутове прискорення.
- кутове прискорення.
Для малих відхилень від положення рівноваги  , і рівняння (2.1) набуде вигляду:
, і рівняння (2.1) набуде вигляду:
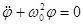 (2.2)
(2.2)
з урахуванням позначення 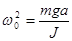 . Розв'язок цього рівняння добре відомий - це гармонічні коливання з частотою
. Розв'язок цього рівняння добре відомий - це гармонічні коливання з частотою 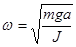 , тобто функція де
, тобто функція де 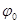 - амплітуда коливань, а
- амплітуда коливань, а 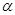 - початкова фаза. Переконайтесь у цьому підставивши запропонований розв’язок (2.3) у рівняння (2.2). Амплітуда
- початкова фаза. Переконайтесь у цьому підставивши запропонований розв’язок (2.3) у рівняння (2.2). Амплітуда
 (2.3)
(2.3)
коливань 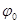 і початкова фаза
і початкова фаза  залежать від того, як збуджуються коливання маятника, тобто визначаються так званими початковими умовами задачі - початковим кутовим відхиленням
залежать від того, як збуджуються коливання маятника, тобто визначаються так званими початковими умовами задачі - початковим кутовим відхиленням  і початковою кутовою швидкістю
і початковою кутовою швидкістю
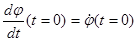
Період коливань 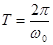 , визначається параметрами маятника та прискоренням сили тяжіння
, визначається параметрами маятника та прискоренням сили тяжіння 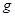 і дорівнює:
і дорівнює:
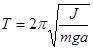 (2.4)
(2.4)
Позначимо через 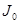 момент інерції маятника відносно осі, що
момент інерції маятника відносно осі, що
|
|
Рис. 2.1. Схема руху маятника
проходить через центр мас С і паралельна до осі коливань. Відповідно до теореми Штейнера:
 (2.5)
(2.5)
звідки
 (2.6)
(2.6)
Формула (2.6) дає залежність періоду коливань 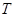 фізичного маятника від відстані "а" між точкою підвісу та центром мас.
фізичного маятника від відстані "а" між точкою підвісу та центром мас.
З'ясуємо поведінку функції T(а) при дуже великих ( ) та малих (а
) та малих (а 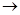 0) значень "a ".
0) значень "a ".
Очевидно, що при 
 , тобто Т~
, тобто Т~  . Аналогічно, при малих значеннях "а"
. Аналогічно, при малих значеннях "а" 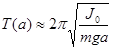 / або
/ або  . У такому
. У такому
|
|
випадку кажуть, що при  період Т (а) —>
період Т (а) —> 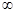 як
як  , при
, при 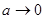 період також прямує до нескінченності, але на цей раз як
період також прямує до нескінченності, але на цей раз як 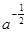 . Функція (2.6) неперервна на (0,
. Функція (2.6) неперервна на (0, 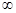 ) і прямує до нескінченності на краях інтервалу.
) і прямує до нескінченності на краях інтервалу.
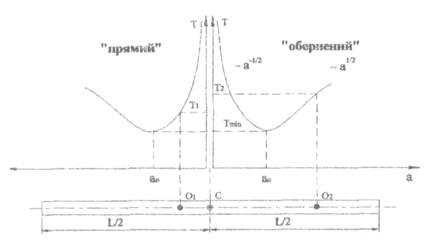
Рис.2.2 Залежність періоду колисань Т фізичного маятника від відстані "а" між точкою підвісу та центром мас.
Відповідно, вона повинна досягати деякого мінімального значення а є (0, 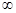 ). (Дослідіть на екстремум підкорінний вираз у формулі (2.6) і покажіть, що мінімальне значення періоду
). (Дослідіть на екстремум підкорінний вираз у формулі (2.6) і покажіть, що мінімальне значення періоду 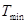 досягається за умови
досягається за умови 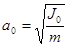 Окрім того, формула (2.6) описує залежність Т (а) як для "прямого", так і для "оберненого" маятника. Усі ці міркування дають змогу дуже просто побудувати графік функції T(а). показаний нарис. 2.2. Осі T на рис 2.2 слід вважати такими, що співпадають. При підвішуванні маятника, наприклад, у точках О
Окрім того, формула (2.6) описує залежність Т (а) як для "прямого", так і для "оберненого" маятника. Усі ці міркування дають змогу дуже просто побудувати графік функції T(а). показаний нарис. 2.2. Осі T на рис 2.2 слід вважати такими, що співпадають. При підвішуванні маятника, наприклад, у точках О 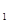 і О2 відповідні періоди дорівнюють Т
і О2 відповідні періоди дорівнюють Т  і Т
і Т  . Для прикладу на рисунку зображено маятник-стержень, але, природно, усі отримані результати стосуються будь-якого фізичного маятника.
. Для прикладу на рисунку зображено маятник-стержень, але, природно, усі отримані результати стосуються будь-якого фізичного маятника.
Для однорідного стержня 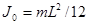 , і формулу (2.6) можна переписати в такому вигляді:
, і формулу (2.6) можна переписати в такому вигляді:
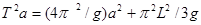 (2.7)
(2.7)
Це дає нам можливість спростити експериментальну перевірку теоретичної залежності T(a), звівши її до простої лінійної функції у змінних Т' 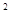 а і
а і 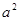 . Графік функції
. Графік функції 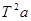 від а2 має вигляд прямої.І кутовим коефіцієнтом
від а2 має вигляд прямої.І кутовим коефіцієнтом
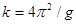 . (2.8)
. (2.8)
Пряма має зсув по осі 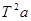 на величину
на величину
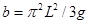 (2.9)
(2.9)
як показано на рис. 2.3.
Якщо, з урахуванням похибки експерименту, отримані точки вкладаються на пряму, то це є свідченням справедливості теоретичної залежності (2.6). У цьому випадку через експериментальні точки можна провести найкращу, тобто найбільш близьку до усіх значень (Т' 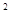 а;
а; 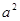 ) пряму, що дасть можливість визначити кутовий коефіцієнт
) пряму, що дасть можливість визначити кутовий коефіцієнт 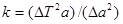 і прискорення сили тяжіння
і прискорення сили тяжіння 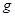 за формулою (2.8). Точками на рис.2. З зображено експериментальні значення (Т'
за формулою (2.8). Точками на рис.2. З зображено експериментальні значення (Т' 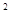 а;
а; 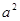 ). Зміщуючи точку підвісу маятника О і вимірюючи відповідні значення "а" і Т, можна зняти експериментальну залежність Т'
). Зміщуючи точку підвісу маятника О і вимірюючи відповідні значення "а" і Т, можна зняти експериментальну залежність Т' 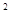 а від
а від 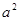 ).
).
 2020-10-12
2020-10-12 193
193