2020-10-12
34
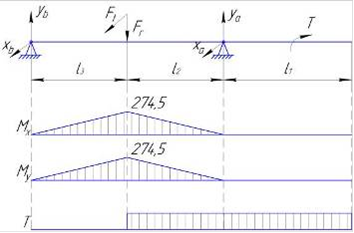
Действующие нагрузки:
Радиальная сила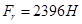 
Крутящий момент -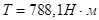 
Момент на барабане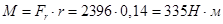 
, 
, 
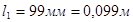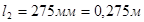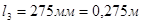
Определим реакции опор в вертикальной плоскости.
. 
, 
.
. 
, 
,
.
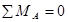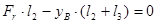
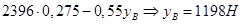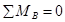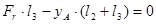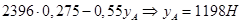Выполним проверку: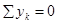 
, 
,
,
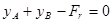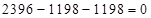Следовательно вертикальные реакции найдены верно.
Определим реакции опор в горизонтальной плоскости.
. 
, 
,
,
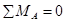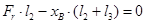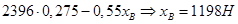получаем, что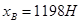 
.
. , 
,
,
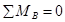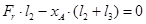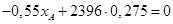отсюда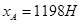 
.
Проверим правильность нахождения горизонтальных реакций: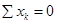 
, 
, 
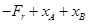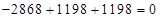, - верно.
Моменты в опасном сечении будут равны:
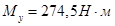
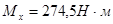
Расчёт производим в форме проверки коэффициента запаса прочности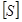 
, значение которого можно принять 
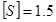. При этом должно выполняться условие, что 
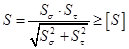, где 
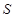- расчётный коэффициент запаса прочност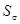и, 
и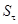 
- коэффициенты запаса по нормальным и касательным напряжениям, которые определим ниже.
Найдём результирующий изгибающий момент, как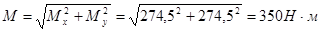 
.
Определим механические характеристики материала вала (Сталь 45):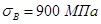 
- временное сопротивление (предел прочности при растяжени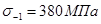и); 
и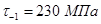 
- пределы выносливости гладких образцов при симметричном цикле изгиба и кручении; 
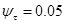- коэффициент чувствительности материала к асимметрии цикла напряжений.
|
|
|
Определим отношение следующих величин:
, 
,
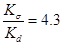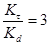где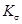 
и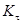 
- эффективные коэффициенты концентрации напряжений, 
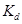- коэффициент влияния абсолютных размеров поперечного сечения. Найдём значение коэффициента влияния шероховатости 
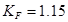и коэффициент влияния поверхностного упрочнения 
.
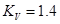Вычислим значения коэффициентов концентрации напряжени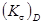й 
и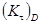 
для данного сечения вала:
,
.
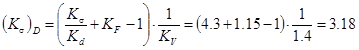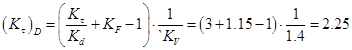Определим пределы выносливости вала в рассматриваемом сечении:
,
.
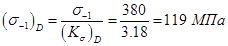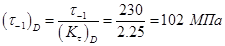Рассчитаем осевой и полярный моменты сопротивления сечения вала:
,
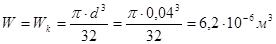где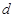 
- расчётный диаметр вала.
Вычислим изгибное и касательное напряжение в опасном сечении по формулам:
,
.
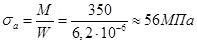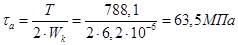Определим коэффициент запаса прочности по нормальным напряжениям:
.
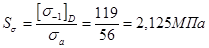Для нахождения коэффициента запаса прочности по касательным напряжениям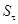 
определим следующие величины. Коэффициент влияния асимметрии цикла напряжений для данного сечения 
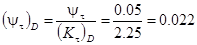. Среднее напряжение цикла 
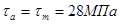. Вычислим коэффициент запаса
.
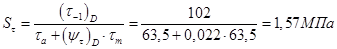Найдём расчётное значение коэффициента запаса прочности и сравним его с допускаемым: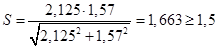 
- условие выполняется.
