Решение.
 — модуль главного вектора. Находим проекции главного вектора на оси координат:
— модуль главного вектора. Находим проекции главного вектора на оси координат:
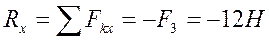
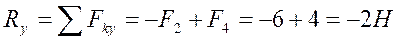

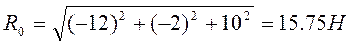
Модуль главного момента
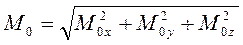
Находим проекции главного момента на оси координат:
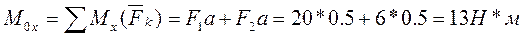
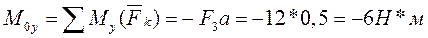
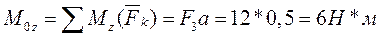
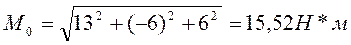
Углы, образованные главным вектором и главным моментом с осями координат:
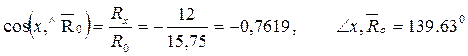
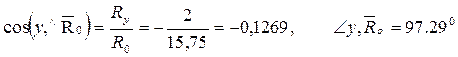
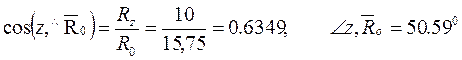
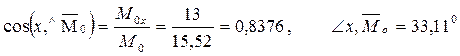

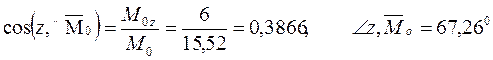
Ответ. R0 = 15,75 Н, М0= 15,52 Н*м.
Условием равновесия пространственной произвольной системы сил является одновременное обращение главного вектора и главного момента системы в ноль:
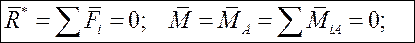
Уравнения равновесия получаются в виде системы шести уравнений из условий равновесия с использованием выражений для проекций главного вектора и главного момента
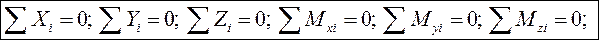
Пример.
Прямоугольная однородная плита весом Р удерживается в горизонтальном положении тросом СС’. Определить реакции связей, если Р= 100 Н, F = 40 Н, а = 30°, 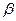 = 60°, F ║ zAy.
= 60°, F ║ zAy.
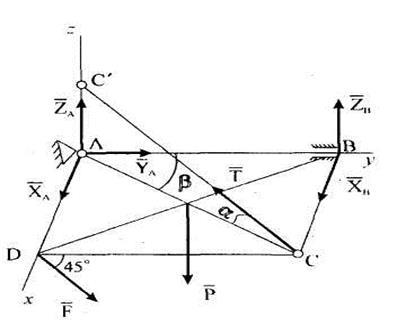 Решение. Используя принцип освобождаемости от связей, заменим действие связей реакциями, приложенными к плите. В точке А (сферический шарнир) будут три составляющие:
Решение. Используя принцип освобождаемости от связей, заменим действие связей реакциями, приложенными к плите. В точке А (сферический шарнир) будут три составляющие: 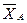 ,
, 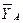 ,
, 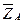 .
.
В точке В — две составляющие: 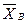 ,
, 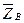 . Реакцию нити
. Реакцию нити  направим по линии СС’. Для уравновешенной произвольной пространственной системы сил составим шесть уравнений равновесия:
направим по линии СС’. Для уравновешенной произвольной пространственной системы сил составим шесть уравнений равновесия:
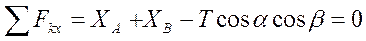
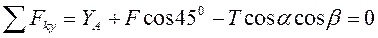
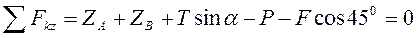
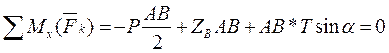
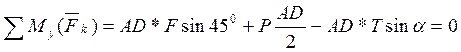
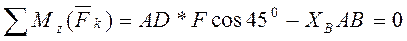
Находим из (6). 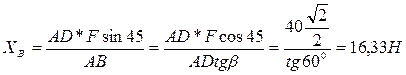
Из (5). 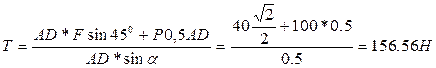
из (4). 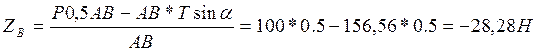
из (1). 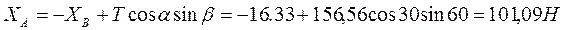
из (2). 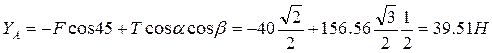
из (3). 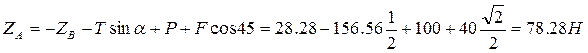
Ответ. ХB= 16,33 H, ZВ = -28,28 H, XA = 101,09 H, YA= 39,51 H, ZA = 78,28 H, T=156,56Н.
Минус показывает, что направление ZB противоположно направлению, показанному на рис.
Равновесие пространственной системы параллельных сил
Для пространственной системы параллельных сил можно составить три уравнения равновесия. Если силы параллельны оси Z, то имеем следующие уравнения равновесия:

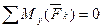
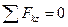
Квадратная однородная плита весом Р находится в равновесии. Определить реакции связей, если P = 100 Н; F = 20 H (рис. 14).
Решение. Рассмотрим равновесие плиты под действием системы параллельных сил 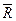 ,
, 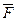 и реакций связей
и реакций связей 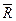 A,
A, 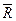 B,
B, 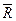 D. Составим три уравнения равновесия:
D. Составим три уравнения равновесия:
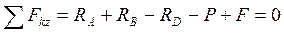
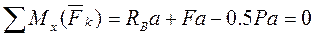
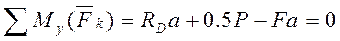
Находим из (2). RB =-F + 0,5P =-20 + 0,5-100 = 30Н,
из (3). RD =-0,5P+F = -0,5 100 + 20 = - 30 Н,
из (1). RA =-RB+RD+P-F = -30-30 +100-20 = 20 H.
Ответ. RA= 20 Н, RB = 30 Н, RD = -30 Н.
Минус показывает, что реакция связей RD направлена противоположно направлению, показанному на рис.
Возможные случаи приведения пространственной произвольной системы сил:
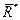
| 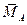
| Дополнительное условие | Простейший вид системы | |
| 1 | 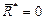
| 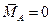
| Условия равновесия | |
| 2 | 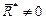
| 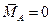
| Равнодействующая | |
| 3 | 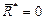
| 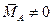
| Пара сил | |
|
4 |
|
| 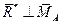
| Равнодействующая |
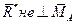
| Силовой винт (сила и пара) | |||
|
| ||||
Пример.
Привести систему сил, действующую на куб, к простейшему виду, если а = 2 м, F1 = 8 Н, F2 = 16 Н, F3 = 8 Н, F4 = 8 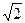 Н (рис. 6).
Н (рис. 6).
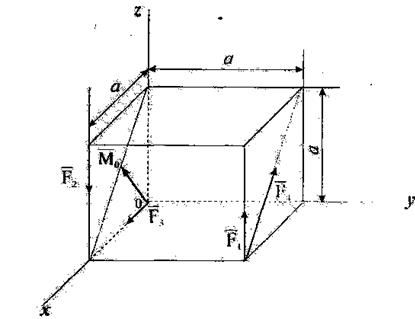
Решение. Определим модуль и направление главного вектора:

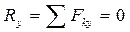
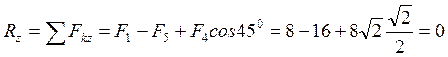
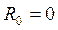
Определим модуль и направление главного момента:
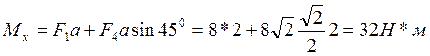

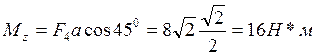
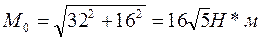
Следовательно, система сил приводится к главному моменту, лежащему в плоскости Oxz. Направление главного момента определяется найденными косинусами.
Приведение к равнодействующей
а) 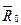
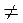 0,
0, 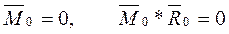
Система сил приводится к равнодействующей, равной главному вектору по модулю и направлению и проходящей через центр приведения.
Пример.
Привести систему сил к простейшему виду, если Р1 = Р2= Р3 = 4 Н, а = 10 м, b = 16 м, с = 6 м.
Решение. Определим модуль и направление главного вектора системы сил:
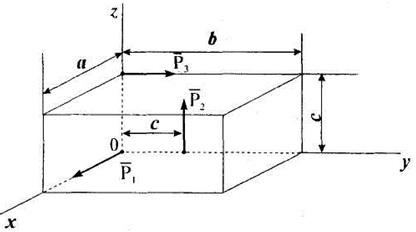
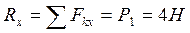

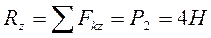
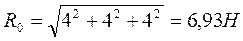

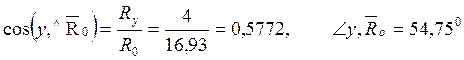
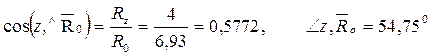
Определим модуль и направление главного момента:
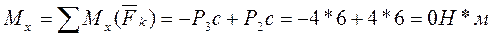
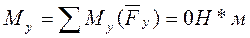
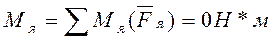

Ответ. Система сил приводится к равнодействующей, линия действия которой проходит через начало координат
б) 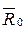
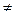 0,
0, 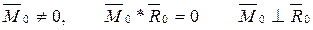 . Система сил приводится к равнодействующей, равной по модулю и направлению главному вектору и отстоящей от центра приведения на расстоянии
. Система сил приводится к равнодействующей, равной по модулю и направлению главному вектору и отстоящей от центра приведения на расстоянии 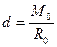 . Линия действия равнодействующей называется центральной осью системы.
. Линия действия равнодействующей называется центральной осью системы.
Пример.
Привести систему сил к равнодействующей, если главный вектор
(Rо = 20 Н) перпендикулярен главному моменту ( M0 = 80 Н*м) в центре приведения O
Решение. Главный момент заменим парой сил (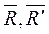 ), сохраняя его величину. Значение силы в паре примем равной величине главного вектора: R = R’ = Ro = 20 Н.
), сохраняя его величину. Значение силы в паре примем равной величине главного вектора: R = R’ = Ro = 20 Н.
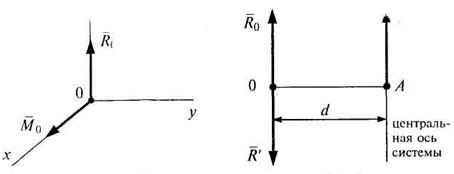
Плечо пары 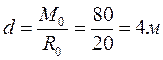
Направление вращения пары соответствует главному моменту. Получим в точке О две равные по модулю и противоположно направленные силы, которые являются уравновешенной системой сил (аксиома 1):
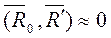 . Следовательно, получим что
. Следовательно, получим что 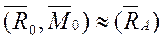
Линия действия равнодействующей в точке А будет центральной осью системы.
Приведение системы сил к динаме (динамическому винту)
Известно, что 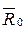
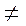 0,
0, 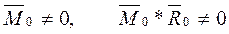
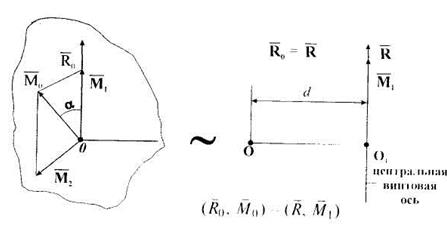 Система сил приводится к динаме (динамическому винту). Динамой называют совокупность силы и пары сил, векторный момент которой направлен параллельно вектору силы. Линию действия динамы называют центральной винтовой осью. Главный момент раскладываем на направление главного вектора и перпендикулярно главному вектору:
Система сил приводится к динаме (динамическому винту). Динамой называют совокупность силы и пары сил, векторный момент которой направлен параллельно вектору силы. Линию действия динамы называют центральной винтовой осью. Главный момент раскладываем на направление главного вектора и перпендикулярно главному вектору: 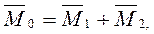 М1=М0 cosa, М2=М0 sina,
М1=М0 cosa, М2=М0 sina,
Так как 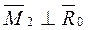 , то эта система сил приводится к равнодействующей, которая находится от точки приведения на расстоянии:
, то эта система сил приводится к равнодействующей, которая находится от точки приведения на расстоянии: 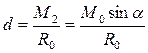
Пара сил с векторным моментом M1=M0cos a является свободным вектором и поэтому поэтому 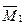 перенесем в точку О1, где приложена равнодействующая. Получим в точке О1, систему, эквивалентную исходной системе сил:
перенесем в точку О1, где приложена равнодействующая. Получим в точке О1, систему, эквивалентную исходной системе сил:
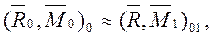 где
где 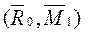 — динама.
— динама.
Пример
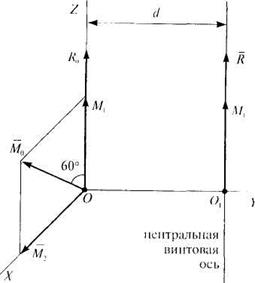
В центре приведения О главный вектор (Rо = 20 Н) и главный момент (Mo = 40 Н*м) расположены в плоскости ZOX и образуют угол в 60°. Определить момент динамы и линию ее действия.
Решение. Момент динамы равен M1=M0cos 600=
=40 * 0,5 = 20 Н*м. Динама отстоит от точки О на расстоянии: 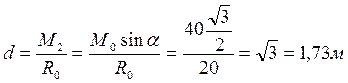
Значение d необходимо откладывать по напралению оси Y в соответствии с правилом знаков для момента 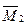 .
.
 2020-10-12
2020-10-12 232
232