Если известны проекции главного вектора и главного момента на оси координат и координаты точки О1, через которую проходит динама, то уравнение центральной винтовой оси в декартовой системе координат имеет вид
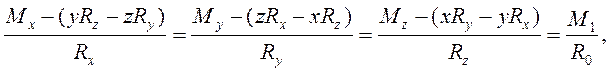
Где: MX, MY, Mz— проекции главного момента; Rx, Rv, Rz — проекции главного вектора; x, у, z координаты точки О1, через которую проходит динама.
Проекция главного момента М1 относительно центра приведения О на направление главного вектора:
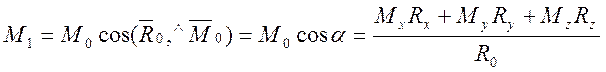
Минимальный главный момент системы сил из скалярного инварианта статики следует: 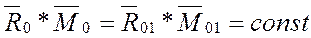 или
или
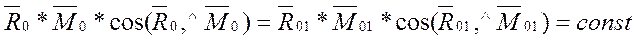
Так как R0=R01, то 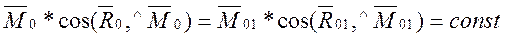 .
.
Из формулы видно, что проекция главного момента на направление главного вектора является постоянной величиной. Если главный момент направлен по главному вектору, то модуль главного момента будет минимальным.
Для системы сил, приводящейся к динаме, проекция главного, момента на направление главного вектора будет минимальным главным моментом системы. Величину минимального главного момента находят по формуле: 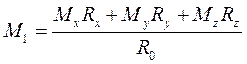 .
.
Инварианты системы сил – величины, не зависящие от выбора центра приведения.
Первый (векторный) инвариант-главный вектор системы сил 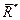
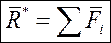
Главный момент не является инвариантом, поскольку он зависит от выбора центра приведения. Однако существует величина, связанная с главным вектором, не зависящая от выбора центра приведения:
1. Запишем зависимость для главного момента системы от выбора точки приведения: 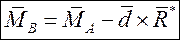
2. Умножим левую и правую части этого выражения скалярно на главный вектор и раскроем скобки: 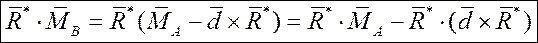
3. Второе слагаемое в правой части обращается в ноль, т.к. главный вектор перпендикулярен вектору векторного произведения в скобках. Отсюда получаем тождество: 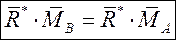
Таким образом, скалярное произведение главного вектора 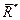 на вектор главного момента есть второй (скалярный) инвариант:
на вектор главного момента есть второй (скалярный) инвариант: 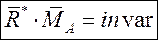 Отсюда,
Отсюда, 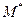 также является инвариантной величиной:
также является инвариантной величиной:
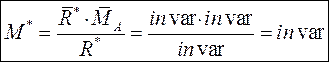
Теоремы Вариньона о моментах равнодействующей для пространственной системы сил:
1.Если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен геометрической сумме моментов сил системы относительно того же центра.
2.момент равнодействующей относительно любой оси равен алгебраической сумме моментов сил системы относительно той же оси.
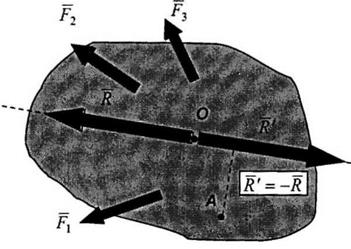
Доказательство: Пусть система сил 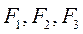 ... приводится к равнодействующей, приложенной в точке О. Такая система не находится в равновесии (
... приводится к равнодействующей, приложенной в точке О. Такая система не находится в равновесии (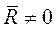 ).
).
Уравновесим эту систему силой 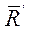 , равной равнодействующей
, равной равнодействующей 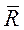 , направленной по линии ее действия в противоположную сторону (аксиома о двух силах).
, направленной по линии ее действия в противоположную сторону (аксиома о двух силах).
Система исходных сил 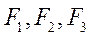 ... и уравновешивающей силы R' находится в равновесии и должна удовлетворять условиям равновесия, например:
... и уравновешивающей силы R' находится в равновесии и должна удовлетворять условиям равновесия, например: 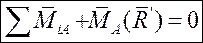
Поскольку сила  , равна равнодействующей
, равна равнодействующей  и направлена по линии ее действия в противоположную сторону, то
и направлена по линии ее действия в противоположную сторону, то 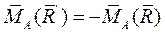 . Подстановка этого равенства в уравнение равновесия дает:
. Подстановка этого равенства в уравнение равновесия дает: 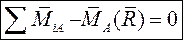 или
или 
Спроектируем это векторное равенство на любую ось, например, х: 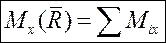
 2020-10-12
2020-10-12 129
129







