Как суммируются пары сил? Чем может быть заменена система пар сил, действующих на твердое тело?

Сложение пар

Пусть даны две пары с моментами m ₁и m ₂, расположенные в пере­секающихся плоскостях (рис.25).

Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: 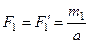, а об­разующих вторую пару: .

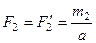Эти пары показаны на рис.25, где 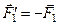, 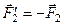. И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересе­чения плоскостей.

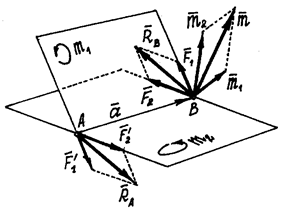
Рис.25

 

Рис. 4.4.

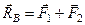Сложив силы, приложенные к точкам А и В, построением паралле­лограммов, получим их равнодействующие и 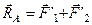. Так как 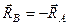, то эти силы 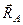и 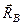будут образовывать пару, мо­мент которой 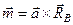, где 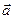– радиус-вектор точки В, совпадающий с АВ.

Так как 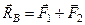, то момент полученной пары

.

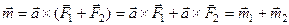Следовательно, в результате сложения пар, расположенных в пере­секающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоско­стях, получим пару с моментом

.                                                                      

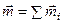Конечно, эта результирующая пара будет располагаться в плоско­сти перпендикулярной вектору .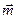

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие рав­новесия пар

.                         

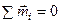Если пары расположены в одной плоско­сти, векторы моментов их будут параллельны. И момент результирующей пары можно опре­делить как алгебраическую сумму моментов пар.

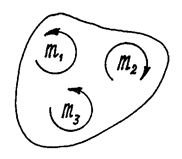
Рис.26

 

Например, пары, показанные на рис.26, расположены в одной плоскости и моменты их:

m ₁=2 Hсм, m ₂=5 Hсм, m ₃=3 Hсм. Пары урав­нове­шива­ются, потому что алгебраиче­ская сумма их моментов равна нулю:

 

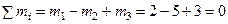
Любая система сил, действующих на АТТ при приведении к произвольно выбранному центру О заменяется одной силой R равной главному вектору систем и приложенный к центру проведения О (R=∑Fi) и одной парой Мо, равной главному моменту сил относительно центра О (Mo(Fi)=∑Mo(Fi)).