Модуль III. Векторные пространства

Лекция 9. Тема: Векторное пространство. Арифметическое векторное пространство

Предметная область лекции (раздела учебной дисциплины): Определение векторного пространства. Простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Арифметическое векторное пространство. Линейная оболочка системы векторов. Система из единичных векторов. Свойства линейной зависимости и независимости системы векторов. Элементарные преобразования над системами векторов. Базис конечной системы векторов. Теоремы о существовании и количестве векторов в базисе.

Цели и технологии их достижения предлагается поставить субъекту учения самостоятельно.

На первой лекции мы ввели понятие алгебры. Изучили алгебру матриц. Для построения алгебры мы предварительно рассматривали поле R – вещественных чисел, хотя можно было рассматривать любое поле.

На этой лекции мы будем строить еще одну алгебру, которую назовем векторным пространством. Для ее построения возьмем поле R (поле вещественных чисел). Будем стоить новую алгебру, элементы которой будем называть векторами, и обозначать а, в, или х, у.

Определение 9.1 (векторного пространства). Векторным пространством над полем R называется алгебра <V, +, λ >, где V – непустое множество элементов любой природы (векторов); операция “+” – сложение векторов из V и операция “λ” – умножение вектора из V на число из поля R, удовлетворяют следующим условиям (аксиомам):

1) сложение векторов коммутативно, т.е. для любых а и в из V: а + в = в + а;

2) сложение векторов ассоциативно, т.е. для любых а, в, с:

а +(в + с) = (а + в) + с;

3) существует в V нулевой вектор, т.е. вектор 0 такой, что для любого а:

а + 0 = 0 + а = а;

4) для каждого вектора а из V существует противоположный вектор, т.е. вектор (– а) такой, что а + (– а) = 0;

5) (λμ) а = λ(μ а) = μ (λ а);

6) (λ + μ) а = λ а + μ а;

7) λ(а + в) = λ а + λ в;

8) 1· а = а.

Легко показать, что алгебра квадратных матриц над полем R образует векторное пространство, т.е. является одним из примеров векторного пространства.

Задание для СУ 9.2. 1. Выучите определение векторного пространства (1 уу). 2. Создайте алгоритм проверки, является ли заданное множество векторным пространством (2 уу). 3. Проверьте, что алгебра квадратных матриц образует векторное пространство (2 уу).

Теорема 9.3 (простейшие свойства векторных пространств). Если V – векторное пространство над полем R, то имеют место следующие свойства:

1. Если а + в = а, то в = 0.

2. 0 а = 0.

3. α 0 = 0.

4. Если а + в = 0, то в = – а. Заметим, что (– а) = (– 1 )а.

5. Если α а = α в, α ≠ 0, то а = в.

6. Если α а = 0, то α = 0 или а = 0.

7. Если α а = β а, а ≠ 0, то α = β.

Доказательство.

(1) Пусть а + в = а, тогда можно к обеим частям равенства прибавить вектор (– а) (такой вектор существует по аксиоме 4): (– а) + а + в = (– а) + а = 0. Учитывая, что (– а) + а = 0, получаем, что в = 0, что и требовалось доказать.

(2) Рассмотрим 0 а и сделаем преобразование: (0 + 0) а, воспользуемся аксиомой 6, получим: 0 а = 0 а + 0 а. По определению нулевого вектора, получаем: 0 а = 0.

(3) Рассмотрим α 0 и как в случае 2 сделаем преобразование и воспользуемся аксиомой 7, получим α 0 = α (0 + 0) = α 0 + α 0. По определению нулевого вектора, получаем: α 0 = 0.

(4) Пусть а + в = 0. Прибавим к обеим частям равенства вектор (– а), получим: (– а) + а + в = (– а) + 0 = – а. Так как (– а) + а = 0, то получаем в = – а.

(5) Пусть α а = α в и α ≠ 0. Так как α ≠ 0, то существует α ^–1. Умножим обе части равенства на α ^–1 ≠ 0, получим α ^–1α а = α ^–1 α в, откуда получаем а = в.

(6) Покажем, что если α а = 0, то либо α = 0, либо вектор а = 0. Если

α ≠ 0, то α ^–1α а = α ^–1 0, откуда получаем: а = 0. Если α = 0, то по свойству 2 свойство 6 верно.

(7) Если α а = β а, а ≠ 0, то прибавим к обеим частям вектор (– β а):

α а + (– β а) = (– β а) + β а = (– β + β) а = 0. Тогда (α – β) а = 0. Так как а ≠ 0, то по свойству 6 (α – β)= 0. Откуда получаем, что α = β.

Математический интерес представляет отношение, в которое вступают векторы из V. Таким отношением является “быть линейно зависимыми или линейно независимыми”. Рассматривая матрицы, мы уже говорили о линейной комбинации строк матрицы и ввели понятие линейной зависимости и независимости строк (столбцов) матрицы. Рассмотрим эти понятия для системы векторов. Пусть дано векторное пространство V над полем R и система векторов (1) а₁, а₂,…, а_n.

Определение 9.4 (линейной комбинации векторов системы). Назовем выражение (2) к₁ а₁ + к₂ а₂ +…+к_n а_n линейной комбинацией векторов системы (1), где числа к₁, к₂,…, к_n называют коэффициентами линейной комбинации.

Определение 9.5 (линейной зависимости и линейной независимости векторов системы). Система векторов (1) называется линейно независимой, если ее линейная комбинация (2) обращается в нулевой вектор только при условии равенства нулю всех коэффициентов; называется линейно зависимой, когда линейная комбинация (2) обращается в нулевой вектор при условии хотя бы одного ненулевого коэффициента.

Рассмотрим особое векторное пространство и дополним свойствами понятие линейной зависимости и независимости системы векторов для векторов этого пространства, не нарушая общности.

Введем предварительно определение прямого произведения множества.

Определение 9.6 (прямого произведения множества на себя).

Прямым произведением множества А на себя называется произведение АхАх…хА = {(а₁, а₂, …, а_n), где а_i – элементы из А}.

Рассмотрим прямое произведение RхRх…хR, где R – поле действительных чисел. Элементы этого произведения назовем n – мерными арифметическими вектором.

Определение 9.7 (n – мерного арифметического вектора). n – мерным арифметическим вектором над полем R называется упорядоченная совокупность (а₁, а₂, …, а_n), где а_i – числа из R. Будем обозначать такие векторы буквами а, в или х, у и т.д.

Рассмотрим множество таких векторов и обозначим это множество через Rⁿ. Убедимся в том, что Rⁿ образует векторное пространство. Для этого введем операции:

“+”: (а₁, а₂,…,а_n) + (в₁, в₂,…. в_n) = (а₁ + в₁, а₂ + в₂, …., а_n + в_n);

“λ”: λ (а₁, а₂,…,а_n) = (λа₁, λа₂,…, λа_n).

Теорема 9.8. Множество арифметических n – мерных векторов Rⁿ образует векторное пространство.

Доказательство. Доказательство теоремы проводится непосредственной проверкой выполнимости всех аксиом определения векторного пространства.

Задание для СУ 9.9. 1. Проверить истинность теоремы 9.8 (2 уу).

Определение 9.10. Векторное пространство Rⁿ, состоящее из арифметических n – мерных векторов называется арифметическим n – мерным векторным пространством.

Определение 9.11 (линейной оболочки системы векторов). Множество всех линейных комбинаций векторов системы а₁, а₂,…, а_k называется линейной оболочкой этой системы и обозначается

L = L(а₁, а₂,…, а_k) = {λ₁ а₁ + λ₂ а₂ +…+ λ_k а_k }.

Легко проверить, что линейная оболочка заданной системы векторов тоже образует векторное пространство.

Задание для СУ 9.12. 1. Запомните все выше изложенные определения (1 уу). 2. Проверьте, что линейная оболочка образует векторное пространство (2 уу).

Определение 9.13 (единичных векторов). Система векторов

(1) е₁ = (1, 0, …, 0), е₂ = (0, 1, …, 0), …, е_n = (0, 0,…, 1) из Rⁿ называется системой единичных векторов.

Предложение 9.14 (о линейной независимости системы единичных векторов). Система единичных векторов (1) линейно независимая.

Доказательство. Воспользуемся определением линейной независимости векторов. Составим линейную комбинацию векторов системы (1) и приравнять ее к нулевому вектору: к₁ е₁ + к₂ е₂ +…+ к_n е_n = 0. Затем, произведя операции, приравняем одинаковые компоненты у получившегося вектора и нулевого: к₁(1, 0,…, 0) + к₂(0, 1,…, 0) +…+ к_n(0, 0,…. 1) = 0. Из того, что к₁1 + … + к_n0 = 0, получаем к₁ = 0. Аналогично можно показать, что остальные коэффициенты тоже равны нулю. Таким образом, линейная комбинация векторов единичных обращается в нулевой вектор при условии равенства нулю всех коэффициентов, что и доказывает линейную независимость векторов системы, состоящей из единичных векторов.

Замечание. Доказательство предложения 9.14. осуществлялось по алгоритму, который может использоваться всякий раз, когда необходимо проверить линейную зависимость и независимость векторов. Он состоит в следующем. Если надо проверить линейную зависимость и независимость некоторой конечной системы векторов, то поступают так:

1. Составляют линейную комбинацию векторов, взяв произвольный набор коэффициентов.

2. Приравнивают полученную линейную комбинацию к нулевому вектору.

3. Находят коэффициенты.

4. По значениям коэффициентов делают вывод:

4.1. Если все коэффициенты равны нулю, то система векторов линейно независимая.

4.2. Если хотя бы один коэффициент отличен от нуля, система векторов линейно зависимая.

Перейдем к рассмотрению свойств линейной зависимости и независимости системы векторов.

Теорема 9.15 ( свойство 1 ). Система векторов, содержащая нулевой вектор, линейно зависима.

Доказательство. Пусть дана система (1) 0, а₂,…, а_n, которая содержит нулевой вектор. Составим линейную комбинацию этих векторов вида

к₁ 0 + 0 а₂ +…+0 а_n. Такая линейная комбинация равна нулевому вектору. Однако в ней коэффициент к₁ ≠ 0, что свидетельствует о линейной зависимости этой векторов системы.

Теорема 9.16 (свойство 2). Если подсистема системы векторов (1) линейно зависимая, то и вся система (1) линейно зависимая.

Доказательство. Пусть дана система векторов (1) а₁, а₂,…, а_n. Пусть ее подсистема (2) а₁, а₂,…, а_m (m < n) линейно зависимая.

Составим линейную комбинацию системы (2) и приравняем ее к нулевому вектору: к₁ а₁ + к₂ а₂ +…+к_m а_m = 0 (3). Так как система (2) линейно зависимая, равенство (3) возможно, если какой-нибудь коэффициент отличен от нуля. Допишем к левой части равенства (3) остальные векторы с нулевыми коэффициентами, от чего равенство не изменится. Тогда получим линейную комбинацию системы векторов (1), в которой есть ненулевой коэффициент. Это подтверждает, что система векторов (1) линейно зависимая.

Теорема 9.17 ( свойство 3 ). Любая подсистема линейно независимой системы линейно независимая.

Доказательство. Это свойство доказывается от противного. Если предположить, что подсистема линейно зависимая, то по свойству (2), система зависимая, а это противоречит условию.

Теорема 9.18 (свойство 4). Если система векторов (1) а₁, а₂,…, а_n, у которой и а₁ ≠ 0, линейно зависимая, то среди данных векторов найдется вектор, который линейно выразится через предшествующие векторы.

Доказательство. Пусть условие теоремы выполнено, т.е. система (1) линейно зависимая с первым отличным от нуля вектором. Тогда существует линейная комбинация к₁ а₁ + к₂ а₂ +…+к_m а_m = 0, где один из коэффициентов отличен от нуля. Будем исследовать коэффициенты, начиная с к_m. Если он отличен от нуля, то вектор а_m легко выразить через остальные:

а_m = – к₁/ к_m а₁ – … – к_m–1/ к_m а_m–1. Если этот коэффициент равен нулю, то будем исследовать коэффициент к_m–1. Пусть отличным от нуля окажется коэффициент к_s. Тогда линейную комбинацию можно записать так:

к₁ а₁ + к₂ а₂ +…+ к_s а_s = 0, откуда получим а_s = (– к₁/к_s) а₁ + …+(– к_s-1/к_s) а_s–1. Проверим, что s ≠ 1. Если окажется, что при исследовании к₁ а₁= 0, то вектор а₁ нулевой, что противоречит условию теоремы. Таким образом, теорема верна.

Теорема 9.19 (свойство 5). Система векторов(1) u₁, u₂,…, u_n и u₁ ≠ 0 линейно зависима тогда и только тогда, когда хотя бы один из векторов системы линейно выражается через остальные.

Доказательство. Теорема состоит из двух теорем – прямой и обратной.

(=>) (прямая теорема): Если система векторов(1) u₁, u₂,…, u_n и u₁ ≠ 0 линейно зависима, то хотя бы один из векторов системы линейно выражается через остальные.

Действительно. Если система (1) линейно зависимая, то по теореме 9.18 найдется вектор, который линейно выражается через предыдущие векторы.

(<=) (обратная теорема): Если хотя бы один из векторов системы (1) линейно выражается через остальные векторы, то эта системалинейно зависима.

Действительно. Если найдется вектор u_к в (1), который линейно выражается через некоторые векторы системы, то его можно представить в виде

u_к = к₁ u₁+…+ к_к-1 u_к. Добавим к правой части остальные векторы с нулевыми коэффициентами, от чего равенство не изменится. Затем перенесем вектор u_к в правую часть с коэффициентом (– 1) . Получим линейную комбинацию векторов данной системы, равную нулевому вектору, причем в ней есть коэффициенты отличные от нуля, что доказывает линейную зависимость системы (1).

Теорема 9.20 (свойство 6). Если система векторов (1) u₁, u₂,…, u_n линейно независимая, а система векторов (2) u₁, u₂,…, u_n, v линейно зависимая, то вектор v линейно выражается через данную систему (1).

Доказательство. По условию система (2) линейно зависимая, следовательно, можно составить линейную комбинацию с хотя бы одним ненулевым коэффициентом: к₁ u₁ + к₂ u₂ +…+ к_n u_n + к_n+1 v = 0. Если коэффициент к_n+1= 0, то, окажется что линейная комбинация система векторов (1) обращается в нулевой вектор с коэффициентом отличным от нуля, что указывает на линейную зависимость системы. А это противоречит условию. Следовательно, коэффициент к_n+1отличен от нуля. Что и позволяет вектор v выразить через данные векторы системы (1):

v = (– к₁/к_n+1) u₁ + (– к₂/к_n+1) u₂ +…+ (– к_n/к_n+1) u_n.

Следствие 9.21 (свойство 7). Если вектор u принадлежит линейной оболочке L(v₁, v₂,…, v_n) (1), а все векторы линейной оболочки (1) принадлежат линейной оболочке L (w₁, w₂,…, w_s) (2), то вектор u принадлежит линейной оболочке (2).

Свойство легко доказывается непосредственной проверкой.

Следствие 9.22 (свойство 8). Если (1) u₁, u₂,…, u_n, u_n₊₁ 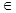L(v₁, v₂,…, v_n), то система (1) линейно зависимая.

Доказательство. Если среди данных векторов системы (1) есть нулевые векторы, то теорема очевидна. Пусть в системе векторов (1) нет нулевых векторов. Продолжим доказательство методом математической индукции.

Пусть все векторы системы (1) отличны от нулевого вектора.

Пусть n = 1, тогда u₁, u₂ 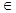L(v₁) => u₁ = в v₁, u₂ = с v₁, где в и с – числа, отличны от нуля, иначе векторы будут нулевыми. Тогда v₁= в^–1 u₁ и v₁= с^–1 u₂ => (в^–1) u₁ + (– с^–1) u₂ = 0, что и подтверждает линейную зависимость системы из двух векторов.

Предположим, что теорема верна для n векторов. Докажем, что теорема верна для n + 1 вектора. Пусть u₁, u₂,…, u_n, u_n+1 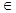L(v₁, v₂,…, v_n). Тогда

u₁ = λ₁₁ v₁ + λ₁₂ v₂ +…    + λ_1n v_n,

           ….................

u_n    = λ_n1 v₁ + λ_n2 v₂ +… + λ_nn v_n,

u_n+1 = λ_n+1,1 v₁ + λ_n+1,2 v₂ +…   + λ_n+1,n v_n.

Если все коэффициенты при v_n равны нулю, то по предположению индукции система векторов, состоящая из n векторов, принадлежит линейной оболочке из n – 1 вектора. Это по предположению индукции означает, что она линейно зависимая. Пусть хотя бы один коэффициент, например λ_n_+1,_nненулевой, тогда исключив вектор v_n из равенств, получим, что n векторов выражаются через

n – 1, что по предположению индукции означает линейную их зависимость, а, следовательно, линейную зависимость данной системы векторов. Что и требовалось доказать.

Следствие 9.23 (свойство 9). Если u₁, u₂,…, u_k_{– 1}, u_к 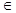L(v₁, v₂,…, v_m), и

к > m, то система векторов u₁, u₂,…, u_k_-1, u_к линейно зависимая.

Истинность следствия непосредственно следует из теоремы 9.22.

Следствие 9.24 (свойство 10). Если u₁, u₂,…, u_k_-–-1, u_к 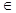L(v₁, v₂,…, v_m) линейно независимая, то к ≤ m.

Истинность следствия непосредственно следует из теоремы 9.22.

Следствие 9.25 (свойство 11). В n – мерном арифметическом векторном пространстве Rⁿ линейно зависима любая система векторов, состоящая из

n + 1 вектора.

Доказательство. Если взять любой вектор из Rⁿ, например вектор

(а₁, а₂,…, а_n), то его можно представить как линейную комбинацию единичных векторов: (а₁, а₂,…, а_n) = а₁(1, 0, …, 0) + а₂(0, 1, …, 0) +…+ а_n(0, 0,…. 1). Следовательно, можно утверждать, что любая система n – мерных векторов u₁, u₂,…, u_n, u_n_{+ 1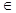} L(e₁, e₂,…, e_n). Тогда по теореме 9.22 и следствию 9.23 система данных векторов линейно зависимая, что и доказывает теорему.

Определение 9.26. Две системы векторов называются эквивалентными, если их линейные оболочки совпадают. Обозначение эквивалентности систем векторов: S₁ ~ S₂. Если системы векторов эквивалентны, то каждый вектор одной системы линейно выражается через векторы второй и обратно.

Над векторами можно производить такие же элементарные преобразования, как мы производили над строками матрицы:

(α): умножение вектора на число, отличное от нуля;

(β): прибавление к одному вектору системы другого, умноженного на число;

(γ): исключение из системы или введение нулевого вектора.

Теорема 9.25. Если одна система векторов получена из другой системы векторов в результате конечной цепочки элементарных преобразований, то эти системы эквивалентны.

Доказательство. Для доказательства утверждения воспользуемся матрицами. Каждый вектор системы можно рассматривать как строку матрицы, а всю систему как матрицу, т.е. А = (А₁, А₂,…, А_m), где А_i – вектор. Матрица, как известно, обладает рангом, указывающим на число линейно независимых ее строк (столбцов). Пусть r (А) = r. Это говорит о том, что число линейно независимых векторов в системе ровно r. Также известно, что элементарные преобразования над строками матрицы не изменяют ее ранга. Следовательно, элементарные преобразования над векторами, тоже не изменят их линейной зависимости и независимости. Проведенные рассуждения позволяют легко получить, что любой вектор А_i 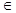L(А₁, А₂,…, А_m) принадлежит линейной оболочке преобразованных векторов: А_i 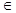L(В₁, В₂,…, В_m) и наоборот. Поэтому линейные оболочки совпадут, что и означает эквивалентность систем данной и полученной конечной цепочкой элементарных преобразований.

Определение 9.26 (базиса системы векторов). Базисом конечной системы векторов называется непустая, линейно независимая ее подсистема, через которую все векторы системы линейно выражаются (или которая эквивалентна данной системе).

Теорема 9.27 (о существовании базиса системы векторов). Конечная система векторов, содержащая хотя бы один ненулевой вектор, обладает базисом. Любые два базиса конечной системы векторов состоят из одинакового числа векторов.

Теорема состоит из двух теорем – теоремы существования и теоремы о количестве векторов в базисе.

Доказательство (теоремы существования). Если система векторов содержит нулевые векторы, то их можно исключить и по теореме 9.26, получится эквивалентная система. Таким образом, есть смысл рассматривать систему без нулевых векторов. Рассмотрим конечную систему векторов, среди которых нет нулевых. Пусть это будет система u₁, u₂,…, u_к (1). Если система (1) линейно независимая, то она непустая, линейно независимая, и каждый ее вектор через нее выражается, поэтому она является базисом данной системы.

Если система (1) линейно зависимая, то по известному свойству найдется вектор, который линейно выражается через предшествующие векторы. Удалим этот вектор из системы, получим систему, эквивалентную данной. После такого преобразования исследуем оставшуюся систему векторов. Если она окажется линейно независимой, то это базис. Если она окажется линейно зависимой, продолжим предыдущее преобразование с оставшейся системой. Так как в системе есть ненулевые векторы, то этот процесс не может быть бесконечным, поэтому базис системы будет найден, что и доказывает существование базис у системы векторов.

Доказательство (теоремы о количестве векторов в базисе). Предположим, что базисов оказалось два: а₁, а₂,…, а_к и в₁, в₂,…, в_s. Тогда, согласно определению базиса: а₁, а₂,…, а_к 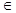L(в₁, в₂,…, в_s) и в₁, в₂,…, в_s 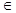L(а₁, а₂,…, а_к). По следствию 9.24, имеем к ≤ s и s ≤ к => s = к, что и требовалось доказать.

Замечание. Система векторов может обладать несколькими базисами, но количество векторов в каждом из них одинаковое.

Теорема 9.28. Арифметическое векторное пространство Rⁿ обладает базисом, состоящим из n векторов.

Доказательство. В Rⁿ система из единичных вектор линейно независимая, состоит она из n векторов, через нее любой вектор линейно выражается. Т.е. система из единичных векторов удовлетворяет всем требованиям базиса, следовательно, она является одним из базисов этого пространства, что и доказывает его существование.

Определение 9.29 (ранга системы векторов). Количество векторов в базисе системы векторов называется рангом этой системы.

Если дана система векторов а₁, а₂, …, а_к, и она линейно независимая, то

ранг r (L) = r (а₁, а₂, …, а_к) = к. Таким образом, r (Rⁿ) = n. В данном случае ранг принят за размерность векторного пространства.

Таким образом, размерность векторного пространства определяется рангом, т.е. количеством векторов в базисе этого пространства, если таковой есть. Ясно, что если S₁ ~ S₂, то r (S₁) = r (S₂).

   Предложение 9.30. Ранг любой системы векторов из n – мерного векторного пространства не превосходит n.

Доказательство. Нами установлено, что любая система из n + 1 вектора линейно зависимая. С другой стороны, ранг Rⁿ равен n. Откуда получаем, что