Пример. Параметр четырёхполюсника, который характеризует его свойства называют передаточный параметр

ЧЕТЫРЕХПОЛЮСНИКА

КОМПЛЕКСНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИ

Параметр четырёхполюсника, который характеризует его свойства называют передаточный параметр.

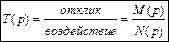
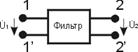
M(p) – полином числителя, N(p) – полином знаменателя, p = j ω – аргумент – комплексная частота.

Физический смысл T(p) зависит от вида отклика – числителя и воздействия – знаменателя.

Наиболее часто рассматриваемым передаточным параметром является коэффициент передачи по напряжению.

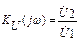
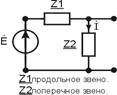Очень многие цепи можно представить в виде так называемого “ Г ”- образного четырехполюсника, который имеет вид

,

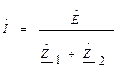
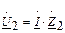
- коэффициент передачи “Г”- образного делителя напряжения равен дроби, в числителе поперечное звено, в знаменателе сумма.

Важно исследовать свойства “ Г ” – образного делителя напряжения, которое определяется соотношением между 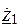и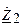

1) Z₁ >> Z₂

Коэффициент передачи меньше единицы.

2) Z₁ = Z₂

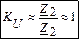
3) Z₁ << Z₂

(чуть меньше единицы)

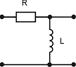Рассмотрим в качестве примера частотные характеристики RL -четырёхполюсника.

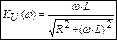
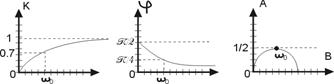
Модуль – АЧХ

Аргумент – ФЧХ

Для построения годографа представим комплексный коэффициент передачи в алгебраической форме

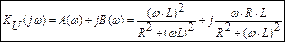
Для построения частотных характеристик составим таблицу

ω	K	φ	A	B
¥

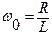
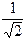
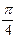
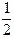
Задание: Самостоятельно рассмотреть частотные характеристики LR -, CR -, RC - четырехполюсников.