Подстановки. Подстановкой называется биекция множества на себя. Подстановка  на множестве
на множестве 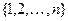 записывается в виде
записывается в виде
 ,
,
при этом 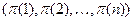 – перестановка элементов
– перестановка элементов 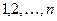 . Подстановка на конечном множестве
. Подстановка на конечном множестве 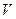 может быть представлена ориентированным графов с множеством вершин
может быть представлена ориентированным графов с множеством вершин 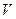 и ребрами
и ребрами 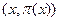 для всех
для всех 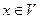 . В этом графе у каждой вершины х полустепени исхода и захода равны 1. Поэтому граф подстановки состоит из непересекающихся ориентированных циклов (в нем могут быть петли – это циклы длины 1). На рисунке 4 показан граф подстановки
. В этом графе у каждой вершины х полустепени исхода и захода равны 1. Поэтому граф подстановки состоит из непересекающихся ориентированных циклов (в нем могут быть петли – это циклы длины 1). На рисунке 4 показан граф подстановки
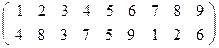 .
.
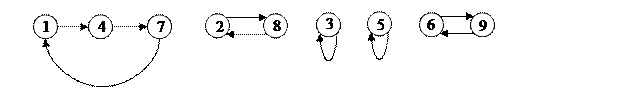
Рис. 4.
Набор чисел  , где
, где 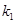 – количество циклов длины 1,
– количество циклов длины 1, 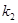 – циклов длины 2,...,
– циклов длины 2,..., 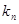 – циклов длины
– циклов длины  , называется цикловой структурой подстановки. Эти числа должны удовлетворять равенству
, называется цикловой структурой подстановки. Эти числа должны удовлетворять равенству 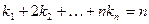 . Число подстановок на множестве из
. Число подстановок на множестве из 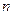 элементов с цикловой структурой
элементов с цикловой структурой  равно
равно
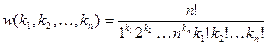 .
.
Автоморфизмы. Автоморфизм – подстановка на множестве вершин графа, сохраняющая отношение смежности (две вершины смежны тогда и только тогда, когда смежны их образы). Иначе говоря, автоморфизм – это изоморфизм графа на себя. Множество автоморфизмов данного графа 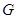 обозначается через
обозначается через 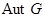 .
.
Каким числом способов можно абстрактный граф с  вершинами превратить в помеченный граф с множеством вершин
вершинами превратить в помеченный граф с множеством вершин 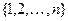 ? Иначе: сколько различных графов можно получить, переставляя пометки вершин у данного помеченного графа
? Иначе: сколько различных графов можно получить, переставляя пометки вершин у данного помеченного графа 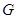 ? Это зависит от графа: из
? Это зависит от графа: из 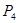 можно получить 12 разных графов, из
можно получить 12 разных графов, из 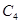 – 8, а для
– 8, а для 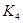 любая перестановка дает тот же самый граф. В общем случае число различных помеченных графов, которые можно получить из графа
любая перестановка дает тот же самый граф. В общем случае число различных помеченных графов, которые можно получить из графа 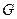 , дает формула
, дает формула
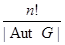 .
.
Орбиты пар. Пусть  – подстановка на множестве
– подстановка на множестве 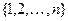 . Относительно этой подстановки множество всех неупорядоченных пар различных элементов из
. Относительно этой подстановки множество всех неупорядоченных пар различных элементов из 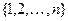 разбивается на орбиты – одну пару можно превратить в другую, действуя на нее (может быть, многократно) подстановкой
разбивается на орбиты – одну пару можно превратить в другую, действуя на нее (может быть, многократно) подстановкой  тогда и только тогда, когда обе пары принадлежат одной орбите. Если
тогда и только тогда, когда обе пары принадлежат одной орбите. Если  является автоморфизмом графа G, то все пары вершин из одной орбиты одновременно смежны или несмежны в этом графе. Обозначим число орбит пар относительно подстановки
является автоморфизмом графа G, то все пары вершин из одной орбиты одновременно смежны или несмежны в этом графе. Обозначим число орбит пар относительно подстановки  через
через 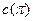 . Любой граф, для которого эта подстановка является автоморфизмом, можно получить следующим образом: каждой орбите приписать одно из значений 0 или 1. Все пары вершин из орбиты объявить смежными, если этой орбите приписана 1, и несмежными, если ей приписан 0. Следовательно, число графов, для которых
. Любой граф, для которого эта подстановка является автоморфизмом, можно получить следующим образом: каждой орбите приписать одно из значений 0 или 1. Все пары вершин из орбиты объявить смежными, если этой орбите приписана 1, и несмежными, если ей приписан 0. Следовательно, число графов, для которых  является автоморфизмом, равно
является автоморфизмом, равно 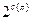 .
.
Число 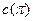 зависит только от цикловой структуры подстановки. Оно равно
зависит только от цикловой структуры подстановки. Оно равно
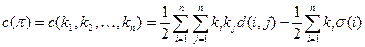 ,
,
где 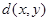 – наибольший общий делитель чисел
– наибольший общий делитель чисел 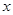 и
и 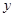 ,
, 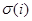 – остаток от деления числа
– остаток от деления числа 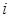 на 2.
на 2.
Число графов. Число абстрактных графов с  вершинами обозначим через
вершинами обозначим через 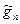 . Построим граф
. Построим граф 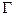 , имеющий вершины двух типов. Вершины первого типа соответствуют графам с множеством вершин
, имеющий вершины двух типов. Вершины первого типа соответствуют графам с множеством вершин 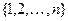 , вершины второго – подстановкам на этом множестве. Вершину-граф соединим ребром с вершиной-подстановкой, если эта подстановка является автоморфизмом этого графа. Подсчитаем двумя способами число ребер в графе
, вершины второго – подстановкам на этом множестве. Вершину-граф соединим ребром с вершиной-подстановкой, если эта подстановка является автоморфизмом этого графа. Подсчитаем двумя способами число ребер в графе 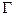 . С одной стороны, подстановка
. С одной стороны, подстановка  является автоморфизмом
является автоморфизмом 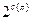 графов. Поэтому число ребер в графе
графов. Поэтому число ребер в графе 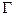 равно
равно
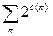 ,
,
суммирование ведется по всем подстановкам на множестве 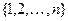 . С другой стороны, из вершины, соответствующей графу
. С другой стороны, из вершины, соответствующей графу 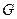 , выходит
, выходит 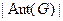 ребер. Объединим все графы, изоморфные графу
ребер. Объединим все графы, изоморфные графу 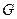 , в один класс, представляющий один абстрактный граф. Из каждой вершины-графа этого класса выходит
, в один класс, представляющий один абстрактный граф. Из каждой вершины-графа этого класса выходит 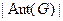 ребер, а всего в классе имеется
ребер, а всего в классе имеется 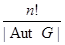 графов. Следовательно, всего из вершин этого класса выходит
графов. Следовательно, всего из вершин этого класса выходит 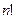 ребер. Так как имеется
ребер. Так как имеется 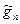 классов, то число ребер в графе
классов, то число ребер в графе 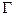 равно
равно 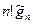 . Получаем равенство
. Получаем равенство
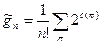 .
.
Учитывая формулу для 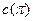 , получаем формулу для числа абстрактных графов:
, получаем формулу для числа абстрактных графов:
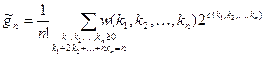 .
.
 2014-02-04
2014-02-04 2413
2413








