Важнейшие классы графов
Задачи
2.1. Сколько имеется неориентированных графов с n вершинами, в которых допускаются
петли?
2.2. Найдите число ориентированных графов с n вершинами, в которых
а) возможны петли;
б) петель нет;
в) петель нет и каждая пара различных вершин соединена не более чем одним ребром;
г) возможны петли и каждая пара вершин соединена не более чем одним ребром;
д) петель нет и каждая пара различных вершин соединена точно одним ребром.
2.3. Найдите число графов с n вершинами, в которых возможны и ориентированные и
неориентированные ребра (но не петли), причем две вершины могут быть соединены
не более чем одним ребром.
2.4. Найдите число неориентированных мультиграфов без петель, в которых для каждой
пары вершин имеется не более четырех соединяющих эти вершины ребер.
2.5. Найдите число графов с n вершинами, в которых а) данные k вершин являются
изолированными (имеют степень 0); б) нет изолированных вершин. Верно ли, что
почти все графы не имеют изолированных вершин?
2.6. Если к графу с 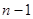 вершиной добавить еще одну вершину и соединить ее ребрами со
вершиной добавить еще одну вершину и соединить ее ребрами со
всеми вершинами нечетной степени, то получится граф с  вершинами, в котором
вершинами, в котором
степени всех вершин четны. Сколько имеется графов, у которых степени всех вершин
четны. Верно ли, что почти все графы имеют вершины нечетной степени?
2.7. Сколько имеется графов с  вершинами, у которых степень каждой вершины равна 1?
вершинами, у которых степень каждой вершины равна 1?
2.8. Сколько различных помеченных графов можно получить, добавляя одно новое
ребро к графу 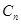 ?
?
2.9. Сколько различных абстрактных графов можно получить, добавляя одно ребро к
графу 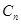 ?
?
2.10. Сколько различных помеченных графов можно получить, добавляя одно ребро к
графу 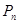 ?
?
2.11. Сколько различных абстрактных графов можно получить, добавляя одно ребро к
графу а)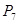 ? б)
? б)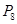 ?
?
2.12. Сколько различных помеченных графов можно получить, перенумеровывая
вершины графа а) 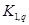 ? б)
? б)  ? в)
? в) 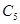 ?
?
2.13. Сколько различных автоморфизмов имеет граф а) 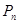 ; б)
; б) 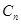 ; в)
; в) 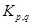 ; г)
; г) 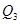 ?
?
2.14. Найдите по возможности малый граф, не имеющий нетривиальных автоморфизмов.
2.15. Опишите единственный нетривиальный автоморфизм графа 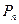 с помощью
с помощью
формулы (нумерация вершин начинается с 1).
2.16. Выразите формулами два автоморфизма графа 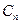 , переводящих вершину i в
, переводящих вершину i в
вершину j (нумерация вершин начинается с 0).
2.17. Пусть 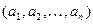 – двоичный вектор. На множестве вершин графа
– двоичный вектор. На множестве вершин графа 
рассмотрим преобразование, переводящее вершину 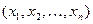 в вершину
в вершину
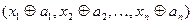 , (
, (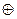 – сумма по модулю 2). Докажите, что оно
– сумма по модулю 2). Докажите, что оно
является автоморфизмом этого графа.
2.18. Примените формулу для числа абстрактных графов при 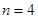 .
.
Деревья
Деревом называется связный граф, не имеющий циклов. Граф без циклов называют лесом.
Во всяком дереве, в котором больше одной вершины, имеется не менее двух вершин степени 1. Такие вершины называют листьями.
Теорема о свойствах деревьев. Если G – дерево, то
1) число ребер в нем на 1 меньше числа вершин;
2) в G любая пара вершин соединена единственным путем;
3) при добавлении к G любого нового ребра образуется цикл;
4) при удалении из G любого ребра он превращается в несвязный граф.
Теорема о центре дерева. Центр любого дерева состоит из одной вершины или из двух смежных вершин.
Центр дерева можно найти следующим образом. Если в дереве больше двух вершин, удалим все его листья. С полученным деревом поступаем так же, это продолжается, пока не останется дерево из одной или двух вершин. Эти вершины и образуют центр исходного дерева.
Наиболее компактным способом представления помеченных деревьев является код Прюфера. Пусть дерево 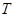 имеет множество вершин
имеет множество вершин 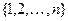 . Код Прюфера этого дерева представляет собой последовательность
. Код Прюфера этого дерева представляет собой последовательность 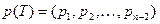 , элементами которой являются вершины. Он строится с помощью следующей процедуры.
, элементами которой являются вершины. Он строится с помощью следующей процедуры.
 2014-02-04
2014-02-04 2269
2269








