Формула дисконтированной (приведенной) стоимости

Формула сложных процентов

Формула простых процентов

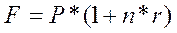
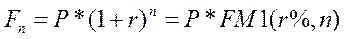
где Р — исходный инвестируемый капитал;

F — размер инвестируемого капитала через n периодов;

r — годовая ставка (требуемая доходность).

FM1(r%,n) — мультиплицирующий множитель для единичного платежа.

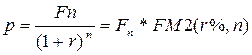
F_n — денежное поступление в году n;

Р — текущая (приведенная) стоимость, т.е. оценка величины F_n с позиции текущего момента;

r — ставка дисконтирования.

FM2(r%,n) — дисконтирующий множитель для единичного платежа. Он показывает «сегодняшнюю» цену одной денежной единицы будущего, т.е. чему с позиции текущего момента равна одна денежная единица через n периодов от момента расчета, при заданных процентной ставке (доходности) r и частоте начисления процента.

В финансовых вычислениях базовым периодом является год, поэтому обычно говорят о годовой ставке. Вместе с тем достаточно широко распространены краткосрочные операции продолжительностью до года. В этом случае за основу берется дневная ставка, причем в зависимости от алгоритмов расчета дневной ставки и продолжительности- финансовой операции результаты наращения будут различными. Используются три варианта расчета: а) точный процент точное число дней финансовой операции; б) обыкновенный процент и точное число дней финансовой операции; в) обыкновенный процент и приблизительное число дней финансовой операции.

Точный процент исчисляется исходя из точного числа дней (365 или 366), а обыкновенный - исходя из приближенного числа дней в году (360). Точное число дней финансовой операции определяется прямым подсчетом, а приблизительное - исходя из предположения, что в месяце 30 дней.