Коэффициент полезного действия (КПД)
Рабочий процесс пароэжекторного вакуумного насоса
Рабочий процесс пароэжекторной ступени можно представить на i –s диаграмме (рис.2).
В идеальном эжекторе без потерь рабочий пар из начального состояния (А) расширяется в сопле адиабатически до давления Р2. Состоянию эжектируемого газа на входе в камеру смешения соответствует точка С, состоянию смеси при изобарическом смешении соответствует точка 3. В диффузоре смесь адиабатически сжимается от давления Р2 (точка 3) до давления Рс (точка 4). В реальном эжекторе все процессы идут с потерями. Процесс смешения не является изобарическим. Состояние смеси в камере смешения характеризуется точкой Д. Сжатие – процесс не адиабатический, и смесь в конце сжатия характеризуется точкой Е.
КПД эжектора, как правило, не входит в расчетные уравнения, но знать его величину необходимо как для понимания сущности процесса, так и для проведения сравнительной технико-экономической оценки различных типов эжекторов, а также для сравнения с другими типами струйных вакуумных насосов.
Сложившаяся практика использует различные оценки энергетической эффективности рабочего процесса пароэжекторного вакуумного насоса.
Более простой и наглядный путь – это непосредственное определение КПД на основе эксергетического метода. Кроме общих балансовых уравнений энергии и массы для термодинамической системы характерен эксергетический баланс независимо от видов энергии, участвующих в процессе:
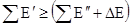 , (2)
, (2)
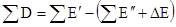 , (3)
, (3)
где индексы «и» означают вход и выход системы.
D – потери эксергии в системе. DЕ = 0 для стационарного процесса.
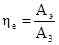 , (4)
, (4)
где Аэ – потоки эксергии, которые определяют полученный эффект.А3 – потоки эксергии,которые определяют затраты.
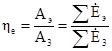 , (5)
, (5)
где  - поток эксергии.
- поток эксергии.
Исходя из этого, рассмотрим процессы в струйном эжекторе. В нем смешиваются потоки, различающиеся по температурам, но главное по давлениям. Схему процесса можно представить следующим образом.

 1 M1; i1; e1; T1; P1
1 M1; i1; e1; T1; P1



 рабочий поток 3 M3; i3; e3; T3; P3
рабочий поток 3 M3; i3; e3; T3; P3
 эжектируемый
эжектируемый
поток 2 M2; i2; e2; T2; P2
Он включает расширение рабочего потока пара от Р1 до Р3 и производимое за счет этого расширения сжатия подсасываемого потока (от давления Р2 до Р3). Изображение этого процесса в координатах i – e представлено на рис. 3. Состояние рабочего пара определяется точкой 1, подсасываемого газа – 2. В идеальном случае состояние смеси отображается точкой 3, находящейся на прямой 1 – 2 (по правилу «рычага»), положение которой определяется соотношением потоков М1 и М2: М2/М1=(1-3)/(2-3).
Потери D в реальном эжекторе приводят к уменьшению давления и эксергии смеси. Действительное состояние пара на выходе из эжектора соответствует точке 3 ’, в которой давление 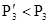 .
.
Коэффициент полезного действия hе процесса в эжекторе определится из соотношения:
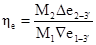 , (6)
, (6)
где D - повышение эксергии, Ñ - понижение.
Несмотря на внешнюю простоту устройства пароструйного эжектора, происходящие в нем термо- и газодинамические процессы сложны и до сих пор полностью не выяснены.
В настоящее время существуют три направления в расчете пароструйных эжекторов.
Первое основано на раздельном рассмотрении процессов расширения, смешения и сжатия с детальной количественной оценкой потерь на каждом этапе рабочего процесса. Для описания происходящих процессов используются термодинамические, газодинамические и тепломассообменные зависимости. Детальное рассмотрение процессов в отдельных элементах проточной части эжектора (сопло, камера смешения, диффузор) является достоинством первого направления, но в то же время неизбежные допущения и упрощения физических представлений настолько снижают точность расчетов, что сложность и громоздкость этих методов становится неоправданной.
Отличительной чертой второго направления является отказ от детальной оценки процессов в отдельных частях проточного тракта эжектора, а рассматриваются процессы в сопле и между двух основных сечений пароэжектора: 1-1 – на выходе их сопла и 3-3 – на входе в диффузор. Второе направление базируется на определенном экспериментальном материале, что коренным образом отличает его от первого направления.
Учитывая сложность газодинамических процессов в сверхзвуковом эжекторе, авторы третьего направления отказываются от выводов громоздких расчетных уравнений. Это направление можно охарактеризовать как эмпирическое. Эмпирическая методика основана на результатах исследования большого количества пароструйных эжекторов. Экспериментально установлено, что расход пара в эжекторе зависит от трех величин: Р0 – начальное давление рабочего пара; Р1 – давление расширения струи в сопле и Р4 – давление на выходе из диффузора, т.е. давление сжатия.
Для практических целей удобно выражать расход пара в зависимости от соотношений между этими величинами, а именно: степени расширения пара в сопле 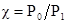 , степени сжатия парогазовой смеси в эжекторе
, степени сжатия парогазовой смеси в эжекторе 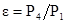 , (Р1 – впускное давление, Р4 – выпускное давление) и коэффициента, равного отношению расхода рабочего пара к расходу эжектируемой смеси
, (Р1 – впускное давление, Р4 – выпускное давление) и коэффициента, равного отношению расхода рабочего пара к расходу эжектируемой смеси 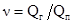
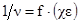 (7)
(7)
Функциональная зависимость (7) графически представлена на диаграмме рис. 4.
 2014-02-02
2014-02-02 5178
5178








