Дифференциальные уравнения равновесия

идеальной жидкости (уравнения Л. Эйлера)

Выделим в покоящейся жидкости элементарный прямоугольный параллелепипед (рис.2), т.е. длины его ребер dx, dy, dz считаем бесконечно малыми величинами. Оси прямоугольных координат направим параллельно ребрам параллелепипеда. В центре тяжести каждой грани параллелепипеда приложим силу гидростатического давления, замещающую действие на нее окружающей массы жидкости. Эти силы согласно первому свойству гидростатического давления будут направлены по нормали внутрь параллелепипеда. Каждая из рассматриваемых сил равна произведению гидростатического давления в центре тяжести данной грани параллелепипеда на ее площадь.

Обозначим гидростатическое давление в центре тяжести параллелепипеда (точка А) через р. Учитывая непрерывность изменения давления в жидкости, т.е. функциональную зависимость (2.2), найдем, что гидростатические давления в центрах тяжести граней параллелепипеда отличаются от давления в точке А соответственно на

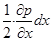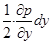; и .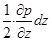

В связи с изложенным силы гидростатического давления будут равны:

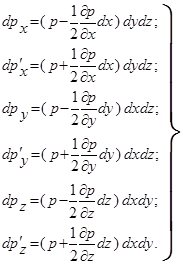(2.3)

Кроме сил гидростатического давления (поверхностных сил) на рассматриваемый параллелепипед действуют массовые силы, непрерывно распределенные по его объему (в данном случае силы тяжести). Равнодействующую массовых сил dG можно представить как произведение ускорения g массовой силы на массу жидкости в объеме параллелепипеда:

dG=g·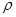·dx·dy·dz, (2.4)

где 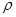– плотность жидкости.

Полагаем, что плотность жидкости постоянна, т.е. 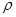=const. Следовательно, жидкость рассматривается как несжимаемая.

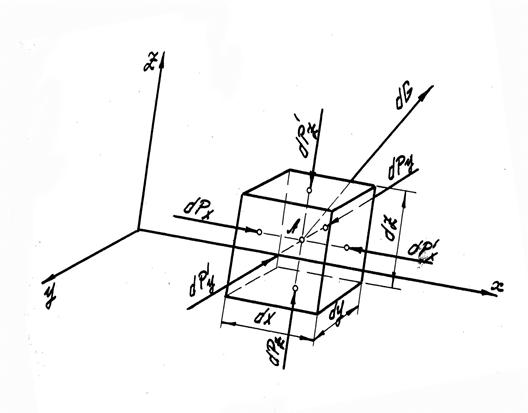
Рис.2

Обозначив проекцию ускорения g на оси О_X, O_Y, О_Z соответственно через X, Y, Z, получим выражения для проекции силы dG на эти оси:

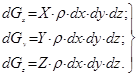(2.5)

Параллелепипед находится в равновесии, поэтому суммы проекции сил на каждую координатную ось должны быть равны нулю. Запишем выражения сумм для каждой оси (О_X, O_Y, О_Z соответственно):

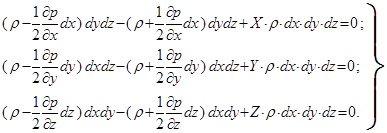(2.6)

Раскрыв скобки и разделив каждое из уравнений на массу параллелепипеда 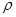dxdydz, т.е. приведя каждый член уравнения к единице массы рассматриваемого объема жидкости, получим систему дифференциальных уравнений равновесия идеальной жидкости:

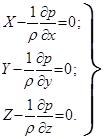(2.7)