2014-02-05
789
Сила абсолютного гидростатического давления
Давление жидкости на плоские поверхности.
Рассмотрим давление жидкости на плоскую стенку произвольного очертания, наклоненную к горизонту под углом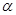 
.Давление на поверхности жидкости равно p0.
Расположим систему координат так, как показано на рис. 7.
Выделим на смоченной части стенки (на рисунке заштрихована) элементарную площадку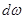 
, центр тяжести которой (точка 
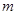) погружен под уровень свободной поверхности на глубине h. Абсолютное гидростатическое давление в центре тяжести площадки 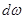ровно p. Тогда сила гидростатического давления на элементарную площадку 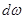составит
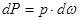. (2.22)
Гидростатическое давление согласно уравнению (2.14)
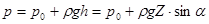. (2.23)
Подставляя эти значения p в уравнение (2.22) и интегрируя его, получаем
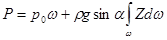. (2.24)
Интеграл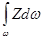 
= Sy представляет статистический момент смоченной поверхности стенки 
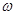относительно оси Oy.
Учитывая, что ордината центра тяжести смоченной поверхности равна Zc , глубина его погружения будет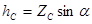 
.
Тогда статический момент смоченной поверхности относительно оси Oy составит
|
|
|
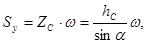(2.25)
и уравнение (2.24) можно записать в виде
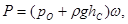
(2.25)
где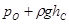 
− есть абсолютное гидростатическое давление в центре тяжести смоченной поверхности.
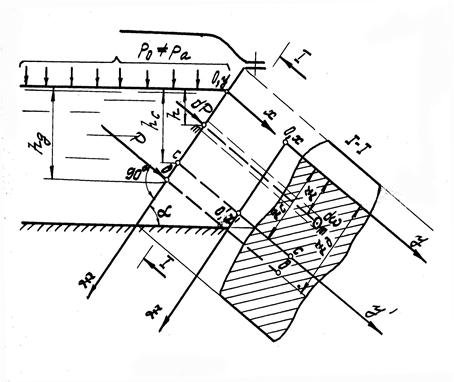
Рис.7
Следовательно, равнодействующая P абсолютного гидростатического давления на плоскую поверхность конечных размеров равна произведению площади смоченной поверхности на абсолютное гидростатическое давление в центре тяжести этой поверхности.
Если p0 равно атмосферному давлению pА, оно уравновешивается таким же давлением на плоскую стенку снизу. В этом случае равнодействующая абсолютного гидростатического давления жидкости будет численно равна силе избыточного (манометрического) давления жидкости на поверхность:
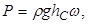(2.26)
где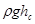 
– избыточное (весовое) гидростатическое давление в центре тяжести смоченной поверхности.
