Б) Объединение множеств.
А) Пересечение множеств.
Определение: Множество состоящее из всех элементов, принадлежащих и множеству А и множеству В, называется пересечением множеств А и В. Обозначают: А 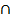 В.
В.
Изображать пересечение множеств можно с помощью кругов Эйлера:
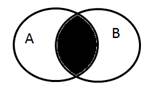
Например:
1. А = {0; 1; 3; 5} и В = {1; 2; 3; 4}
А 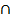 В = {1; 3}
В = {1; 3}
2. [а; в] 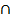 [а; в) = [а; в)
[а; в) = [а; в)
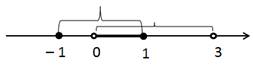
3. [– 1; 1] ∩ (0; 3) = (0; 1]
4. Пересечением множества прямоугольников и множества ромбов является множество квадратов.
Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются (т.е. пересечение 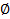 ), т.е. А
), т.е. А 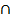 В =
В = 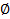 – непересекающиеся множества.
– непересекающиеся множества.
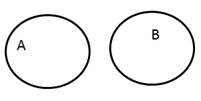
Пересечение любого множества А с пустым множеством есть пустое множество, т.е. А 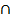
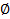 =
= 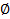 .
.
Определение: Множество состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В. Обозначают: А 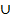 В.
В.
Изображение с помощью кругов Эйлера:
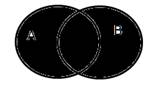
Например:
1. А = {0; 1; 3; 5} и В = {1; 2; 3; 4}
А 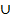 В = {0; 1; 3; 5; 2; 4}
В = {0; 1; 3; 5; 2; 4}
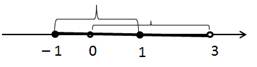
2. [– 1; 1] ∩ (0; 3) = [ – 1; 3)
3. А – учащиеся школы моложе 12 лет,
В – учащиеся школы старше 10 лет
А 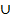 В = {все учащиеся школы}.
В = {все учащиеся школы}.
Если множества А и В имеют элементы, то А 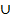 В
В 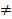
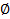 ; А
; А 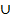
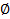 = А.
= А.
Свойства объединения и пересечения множеств.
А ∪ В = В ∪ А
А 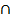 В = В
В = В 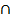 А
А
 2014-02-05
2014-02-05 529
529







