Архитектура кластерной системы (способ соединения процессоров друг с другом) в большей степени определяет ее производительность, чем тип используемых в ней процессоров. Критическим параметром, влияющим на величину производительности такой системы, является расстояние между процессорами. Так, соединив вместе 10 персональных компьютеров, мы получим систему для проведения высокопроизводительных вычислений. Проблема, однако, будет состоять в поиске наиболее эффективного способа соединения стандартных средств друг с другом, поскольку при увеличении производительности каждого процессора в 10 раз производительность системы в целом в 10 раз не увеличится.
Рассмотрим для примера задачу построения симметричной 16-процессорной системы, в которой все процессоры были бы равноправны. Наиболее естественным представляется соединение в виде плоской решетки, где внешние концы используются для подсоединения внешних устройств (рис.2.4).
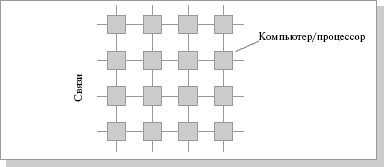
Рисунок 2.4 - Схема соединения процессоров в виде плоской решетки
При таком типе соединения максимальное расстояние между процессорами окажется равным 6 (количество связей между процессорами, отделяющих самый ближний процессор от самого дальнего). Теория же показывает, что если в системе максимальное расстояние между процессорами больше 4, то такая система не может работать эффективно. Поэтому при соединении 16 процессоров друг с другом плоская схема является нецелесообразной. Для получения более компактной конфигурации необходимо решить задачу о нахождении фигуры, имеющей максимальный объем при минимальной площади поверхности. В трехмерном пространстве таким свойством обладает шар. Но поскольку необходимо построить узловую систему, вместо шара приходится использовать куб (рис.2.5), если число процессоров равно 8) или гиперкуб (рис.2.6), если число процессоров больше 8. Размерность гиперкуба будет определяться в зависимости от числа процессоров, которые необходимо соединить. Так, для соединения 16 процессоров потребуется четырехмерный гиперкуб. Для его построения следует взять обычный трехмерный куб, сдвинуть в нужном направлении и, соединив вершины, получить гиперкуб размером 4.
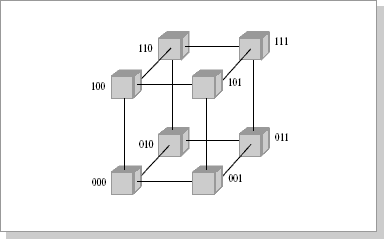
Рисунок 2.5 - Топология связи, 3-х мерный гиперкуб
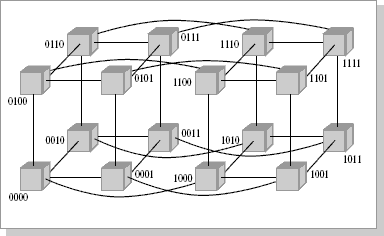
Рисунок 2.6 -Топология связи, 4-х мерный гиперкуб
Архитектура гиперкуба является второй по эффективности, но самой наглядной. Используются и другие топологии сетей связи: трехмерный тор, "кольцо" (рис.2.7), "звезда" и другие.
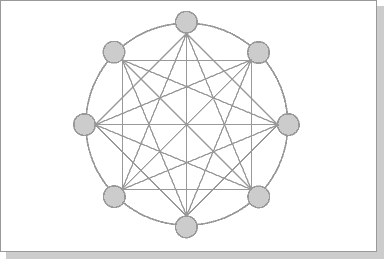
Рисунок 2.7 - Архитектура кольца с полной связью по хордам (Chordal Ring)
Наиболее эффективной является архитектура с топологией "толстого дерева" (fat-tree) (рис.2.8, 2.9). Архитектура "fat-tree" (hypertree) была предложена Лейзерсоном (C.E. Leiserson) в 1985 году. Процессоры локализованы в листьях дерева, в то время как внутренние узлы дерева скомпонованы во внутреннюю сеть. Поддеревья могут общаться между собой, не затрагивая более высоких уровней сети.
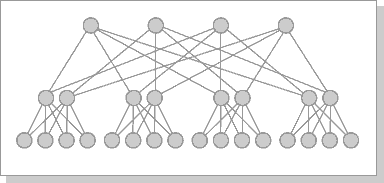
Рисунок 2.8 - Кластерная архитектура "Fat-tree"
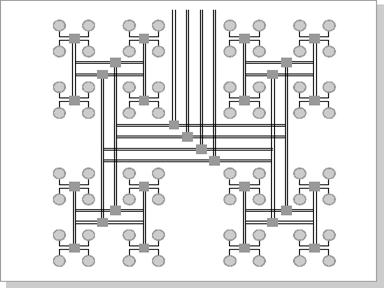
Рисунок 2.9 - Кластерная архитектура "Fat-tree" (вид сверху схему)
Поскольку способ соединения процессоров друг с другом больше влияет на производительность кластера, чем тип используемых в ней процессоров, то может оказаться более целесообразным создать систему из большего числа дешевых компьютеров, чем из меньшего числа дорогих. В кластерах, как правило, используются операционные системы, стандартные для рабочих станций, чаще всего свободно распространяемые (Linux, FreeBSD), вместе со специальными средствами поддержки параллельного программирования и балансировки нагрузки. При работе с кластерами, так же, как и с MPP-системами, используют так называемую Massive Passing Programming Paradigm – парадигму программирования с передачей данных (чаще всего – MPI). Умеренная цена подобных систем оборачивается большими накладными расходами на взаимодействие параллельных процессов между собой, что сильно сужает потенциальный класс решаемых задач.
 2014-02-02
2014-02-02 1895
1895
