Графическими методами решаются задачи второго типа - “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала, а также НС обмоток. Требуется найти значения потоков (индукций) на отдельных участках магнитопровода.
Данные методы основаны на графическом представлении вебер-амперных характеристик 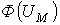 линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
1. “Обратная” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности:
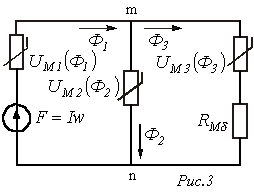 1. Задаются значениями потока и определяют для них НС
1. Задаются значениями потока и определяют для них НС  , как при решении “прямой” задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить
, как при решении “прямой” задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить 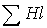 , несколько меньшую и несколько большую заданной величины НС.
, несколько меньшую и несколько большую заданной величины НС.
2. По полученным данным строится часть характеристики 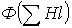 магнитной цепи (вблизи заданного значения НС), и по ней определяется поток, соответствующий заданной величине НС.
магнитной цепи (вблизи заданного значения НС), и по ней определяется поток, соответствующий заданной величине НС.
При расчете неразветвленных магнитных цепей, содержащих воздушные зазоры, удобно использовать метод пересечений, при котором искомое решение определяется точкой пересечения нелинейной вебер-амперной характеристики нелинейной части цепи и линейной характеристики линейного участка, строящейся на основании уравнения
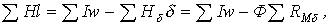
где 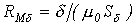 -магнитное сопротивление воздушного зазора.
-магнитное сопротивление воздушного зазора.
2. “Обратная” задача для разветвленной магнитной цепи
Замена магнитной цепи эквивалентной электрической схемой замещения (см. рис. 3, на котором приведена схема замещения магнитной цепи на рис. 2) позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
В этом случае при расчете магнитных цепей, содержащих два узла (такую конфигурацию имеет большое число используемых на практике магнитопроводов), широко используется метод двух узлов. Идея решения данным методом аналогична рассмотренной для нелинейных резистивных цепей постоянного тока и заключается в следующем:
1. Вычисляются зависимости 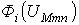 потоков во всех
потоков во всех 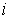 -х ветвях магнитной цепи в функции общей величины -магнитного напряжения
-х ветвях магнитной цепи в функции общей величины -магнитного напряжения 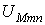 между узлами
между узлами 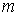 и
и 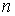 .
.
2. Определяется, в какой точке графически реализуется первый закон Кирхгофа 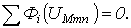 Соответствующие данной точке потоки являются решением задачи.
Соответствующие данной точке потоки являются решением задачи.
 2014-02-02
2014-02-02 518
518








