Статическая и дифференциальная индуктивности катушки с ферромагнитным сердечником

Пусть имеем катушку с ферромагнитным сердечником, представленную на рис. 4.

В соответствии с определением потокосцепления

,

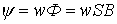(2)

и на основании закона полного тока 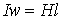, откуда

.

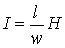(3)

Из соотношений (2) и (3) вытекает, что функция 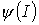качественно имеет такой же вид, что и 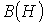. Таким образом, зависимости относительной магнитной проницаемости 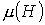и индуктивности 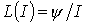также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые 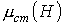и 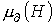качественно аналогичны кривым 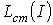и .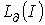

Статическая индуктивность катушки с ферромагнитным сердечником

;

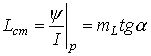дифференциальная индуктивность

.

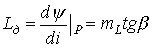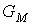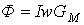Если магнитную проводимость сердечника на рис. 4 обозначить через , то и 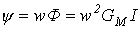, откуда

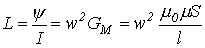(4)

Используя соотношение (4), покажем влияние воздушного зазора на индуктивность катушки.

Пусть катушка на рис. 4 имеет воздушный зазор . Тогда полное магнитное сопротивление контура

,

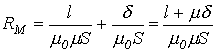откуда

.

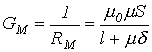При 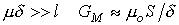, следовательно

.

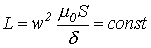Таким образом, воздушный зазор линеаризует катушку с ферромагнитным сердечником. Зазор, для которого выполняется неравенство 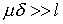, называется большим зазором.