Расчет магнитной цепи машины постоянного тока

Смешанная (лягушечья) обмотка

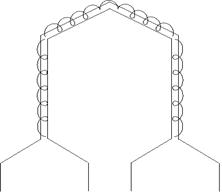
Секции этой обмотки представляют собою комбинацию простых обмоток (петлевой и волновой), рис. 173, а. Эта обмотка применяется для машин большой мощности. В этой обмотке уравнительные соединения не нужны.

В роли уравнителя первого рода служит секция волновой обмотки, в роли уравнителя второго рода служит секция петлевой обмотки.

Рис. 173, а

Расчет магнитной цепи машины постоянного тока сводится к тому, чтобы определить намагничивающую силу необходимую для создания в воздушном зазоре потока 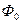, который создает заданную ЭДС в обмотке якоря.

Магнитную цепь обычно рассчитывают на пару полюсов. Так как участки магнитной цепи имеют различное сечение и выполнены из различных материалов то считают, что на каждом участке напряженность магнитного поля постоянная.

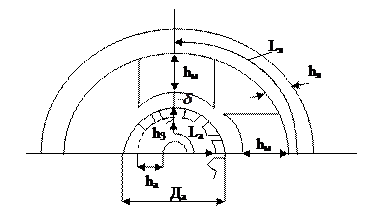Рис. 174

При расчете магнитной цепи рассматривают следующие участки:

1. воздушный зазор - ,
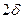2. зубцовая зона якоря - ,
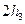3. спинка якоря - ,
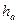4. полюса - ,
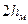5. ярмо станины - .

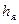Магнитная цепь на пару полюсов представлена на рис. 174.

1. Расчет магнитного напряжения воздушного зазора.

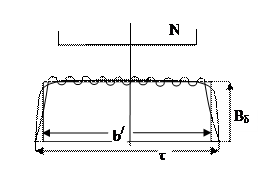
При зубчатом якоре индукция имеет сложный характер (рис…). Действительную картину магнитной индукции заменяют равновеликим прямоугольником (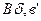), где

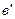- расчетная величина полюсной дуги

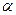- расчетный коэффициент полюсной дуги

Рис. 175

().

, .

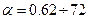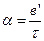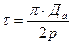Распределение индукции вдоль оси представлено на рис. 176.

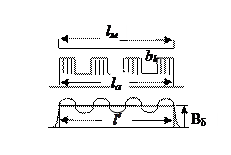
Где: 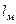- длина полюса,

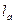- длина якоря,

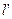- расчетная длина якоря,

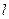- длина без вентиляционных каналов.

, .

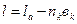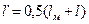Рис. 176

Гладкий якорь.

Поток 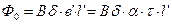, откуда 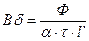, т.к. 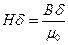, то магнитное напряжение гладкого якоря равно .

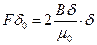Зубчатый якорь.

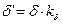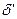Зубчатый якорь при расчете приводят к гладкому, при этом , где - расчетная величина зазора, 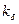- коэффициент зазора

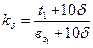, тогда магнитное напряжение зубчатого якоря определится

.

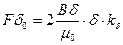2. Магнитное напряжение зубцовой зоны, рис. 177.

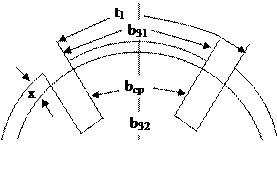
Магнитное напряжение зубцовой зоны рассчитывают на одно зубцовое деление.

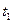- зубцовое деление, .

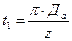Считается, если индукция зубца 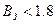Тл, то весь поток зубцового деления проходит через зубец, а если 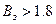Тл, то часть потока проходит через зазор, т.е. .

Рис. 177

Разделим это выражение на 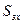, получим 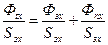, где

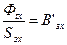- расчетная величина индукции, 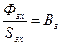- реальная индукция зубца,

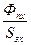- индукция в пазу. Запишем 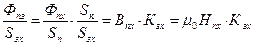, так как

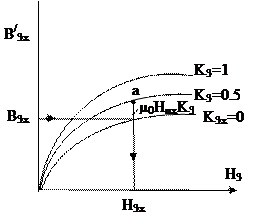
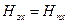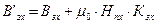, то , где 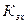- зубцовый коэффициент.

По этой формуле строится зависимость 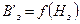при различных коэффициентах 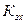., рис. 178

По заданной 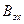определяется 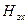и 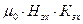(точка ).

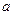Рис. 178

Расчетная индукция исходит из того, что весь поток зубцового деления проходит через зубец, т.е. .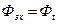

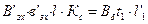, откуда 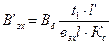, где .

.

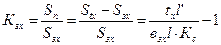Находим расчетную индукцию для трех значений зубца (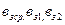) при различных коэффициентах 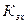(рис…).

, , .

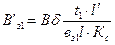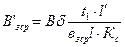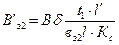Зная марку стали, определяем напряженность для трех значений зубца.

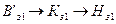, определяем расчетную напряженность зубца.

,

.

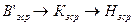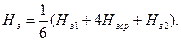
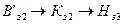Магнитная напряженность зубцовой зоны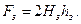

3. Магнитное напряжение спинки якоря.

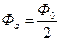, индукция спинки якоря .

Для данной марки стали определяем .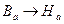

Магнитное напряжение спинки якоря 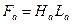, где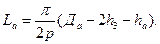

4.Магнитное напряжение полюсов и ярма.

Поток полюса 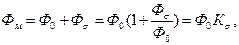где 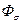- поток рассеяния,

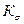- коэффициент рассеяния. ().

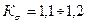Индукция полюса 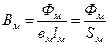, зная материал полюса по .

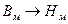Магнитное напряжение полюса .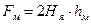

Поток ярма 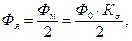индукция ярма

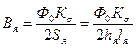, по .

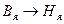Магнитное напряжение ярма 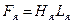, где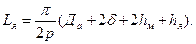

Определяем намагничивающую силу на пару полюсов 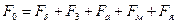, по заданной ЭДС 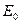определяем поток ,

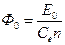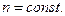
Задавшись различными значениями потока 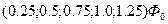определяем 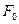и стоим кривую намагничивания, рис. 179.

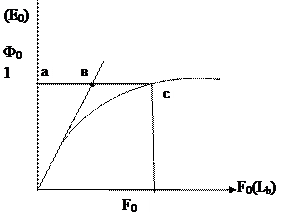Где 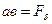, коэффициент насыщения.

, ,

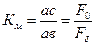получим характеристику холостого хода, зная 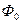и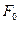

, , .

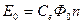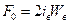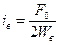Рис. 179

Итак, рассчитав магнитную цепь на пару полюсов, определяем намагничивающую

силу 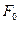необходимую для проведения заданного магнитного потока 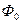по всем участкам магнитной цепи.