Производить операции умножения, сложения и т.п. с токами и напряжениями, изображенными в виде волновых диаграмм, неудобно. Поэтому на практике синусоидальные величины представляют в виде векторов, а затем указанные операции производят с ними. Это значительно упрощает расчеты и делает их более наглядными.
Представление синусоиды в виде волновой диаграммы и вращающегося вектора показано на рисунке.
Вращая вектор I против часовой стрелки его конец будет описывать окружность. При вращении вектора с частотой w его проекция на вертикальную ось изменяется по синусоидальному закону и равна мгновенному значению синусоиды в соответствующие моменты времени. Хорошо видны следующие аналогии:
 Рис. 12 Рис. 12 |
− длина вектора равна амплитуде синусоиды;
− угол между горизонтальной осью и вектором равен начальной фазе синусоиды.
В электротехнике векторы изображают не вращающимися, а неподвижными, для момента времени t =0 и их масштабы выбирают так, чтобы длина вектора соответствовала не амплитуде, а действующему значению. Угол наклона к оси абсцисс равен начальной фазе. Учитываемые параметры (действующее значение и начальная фаза) полностью определяют синусоидальную функцию и позволяют для любого вектора восстановить ее и наоборот.
|
|
|
Так можно представить целую совокупность различных величин u, i, e. Если эти величины одинаковой частоты, то их совокупность представляет собой векторную диаграмму.
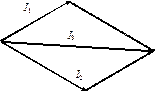 Рис. 13 Рис. 13 |
На рисунке для примера представлена совокупность векторов I 1 и I 2, а также результирующий вектор I 3, определяемый их суммой. Угол измеренный между векторами называют углом сдвига фаз. Если угол между двумя векторами равен нулю, то говорят, что они совпадают по фазе. Если угол равен 180°, то говорят, что векторы находятся в противофазе.
Комплексный метод расчета
Все графические методы расчета электрических цепей синусоидального тока, в том числе и метод векторных диаграмм, не могут обеспечить высокой точности или очень сложны и трудоемки. Комплексный метод расчета, базирующийся на теории комплексных чисел, довольно прост и позволяет добиваться высокой точности.
Любой вектор на плоскости, проведенный из начала координат и изображающий действующее значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка А на рисунке). На плоскости комплексных чисел точке А соответствует одно комплексное число А.
 Рис. 14 Рис. 14 |
Таким образом, любой вектор однозначно изображается комплексным числом, соответствующим концу этого вектора.
Комплексное число имеет вещественную и мнимую составляющие:
|
|
|
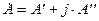 ,
,
где А' — координата точки А на вещественной оси; А" координата точки А на мнимой оси; 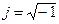 .
.
Умножение какого-то числа на j означает поворот его на угол p/2 по отношению к положительному направлению вещественной оси в направлении против часовой стрелки.
Координаты точки А могут быть выражены через длину вектора |ОА|= А и угол j: А' = А соsj, А" = А sinj. Тогда комплексное число можно записать следующим образом:
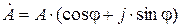 ,
,
где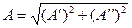 - модуль комплексного числа, равный длине вектора ОА;
- модуль комплексного числа, равный длине вектора ОА; 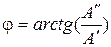 - аргумент комплексного числа, т. е. угол, на который вектор ОА повернут по отношению к положительному направлению вещественной оси.
- аргумент комплексного числа, т. е. угол, на который вектор ОА повернут по отношению к положительному направлению вещественной оси.
Используя формулу Эйлера 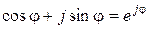 , получим
, получим
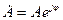 .
.
Таким образом, вектор, расположенный в комплексной плоскости, представлен тремя различными формами записи: алгебраической, тригонометрической и показательной.
Над комплексными числами, изображающими символически векторы ЭДС, напряжений и токов, можно производить все алгебраические действия. При сложении и вычитании удобнее пользоваться алгебраической формой записи, а при умножении, делении, возведении в степень и извлечении корней - показательной.
Так сложение (вычитание) двух комплексных чисел осуществляется в алгебраической форме их представления сложением (вычитанием) соответственно их действительных и мнимых частей:
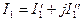
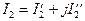
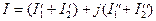 .
.
Умножение (деление) двух комплексных чисел осуществляется в показательной форме их представления по следующим правилам. Модуль результирующего числа равен произведению (частному от деления) модулей исходных чисел, а аргумент - равен сумме (разности) аргументов исходных чисел:

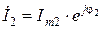
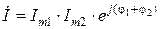 . Для перехода от одной формы записи комплексного числа к другой используют тригонометрическую форму представления:
. Для перехода от одной формы записи комплексного числа к другой используют тригонометрическую форму представления:
 ,
, 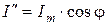 ,
,
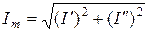 ,
, 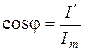 ,
, 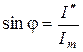 ,
,
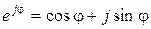 .
.
 2014-02-02
2014-02-02 2353
2353
