Синусоидально изменяющиеся величины характеризуются следующими основными параметрами:
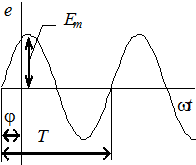 Рис. 11 Рис. 11 |
− период Т, [c] - время совершения одного полного колебания синусоидальной величины;
− частота f, [c-1]=[Гц] - количество периодов, укладывающихся в единицу времени:
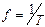 .
.
В нашей стране частота тока в сети f =50 Гц;
− амплитуда Im, Em, Um - наибольшее значение синусоидальной величины. Амплитудные значения синусоидальных функций являются постоянными величинами, т.е. от времени они не зависят.
− мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени. Зависимость их от времени выражается соотношениями:
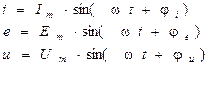 ;
;
− фаза - аргумент синусоидальной функции (w t +j) - показывает, какое значение имеет синусоидальная функция в данный момент времени;
− начальная фаза j - показывает, какое значение имеет синусоидальная функция в момент на чала отсчета, т.е. при t =0;
− угловая (циклическая) частота изменения тока:
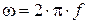 , рад/c.
, рад/c.
Для нашей сети w=314 рад/c.
− Действующее значение переменного тока.
Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:
 |
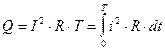 .
.
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
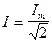 .
.
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
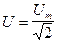
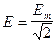 .
.
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение фазного напряжения Um=U Ö2=307 В. Связь между действующим и амплитудным значениями напряжений важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
 2014-02-02
2014-02-02 4871
4871
