Дерево вывода – это множество объединенных правил, отражающих условия выполнения некоторого процесса.
Правила представляют собой языковую конструкцию вида:
ЕСЛИ <условие, ct(условия)>, ТО <заключение, ct(заключения)> ct(правила),
где
ct(условия) – коэффициент определенности условия;
ct(заключения) - коэффициент определенности заключения;
ct(правила) - коэффициент определенности правила.
Коэффициент ct
равный 0, указывает на полную неопределенность,
равный 1 – на полную определенность.
Правила и коэффициенты задает эксперт.
Множество правил объединяются в дерево вывода.
Например задано два правила.
Правило 1.
ЕСЛИ
индекс цен возрастет не менее чем на 3% (условие В) ct(В)
И
цены на энергоносители вырастут не более чем на 19% (условие С), ct(С) = 0,4
ТО акции покупать (заключение А) ct(А) =0,7, ct(правила 1) = 0,7.
Правило 2.
ЕСЛИ ВВП возрастет не менее чем на 1,5% (условие Д) ct(Д) = 0,8
ИЛИ
ставки Центрального банка будут в пределах 12% (условие Е) ct(Е) = 0,5
ИЛИ
объем экспорта возрастет более чем на 5% (условие G) ct(G) = 0,6
ТО индекс цен возрастет не менее чем на 3%. (заключение В) ct(В) = 0,3, ct(правила 2) = 0,3.
Эти правила объединяются в дерево, представленное на рисунке ниже.
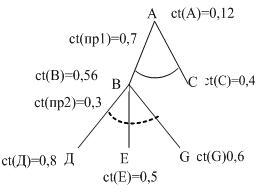
Знания такого рода представляются графически, а также как рассчитывается коэффициент определенности заключения.
Условимся заключение, получаемое с помощью правила, изображать сверху, а условия - снизу.
Число рядом с условием указывает на его определенность, а число рядом с линией - на определенность самого правила.
Условий в правиле может быть несколько, которые связанны между собой союзами И или ИЛИ.
Например
ЕСЛИ А и В и С, ТО Е,
ЕСЛИ А или В или С, ТО Е.
Графически эти правила изображаются так, как это показано на рисунке
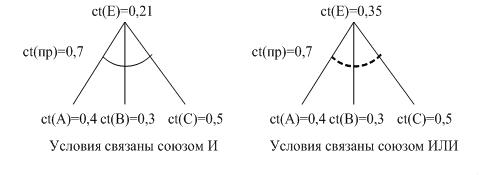
Сплошная или пунктирная дуга указывает на вид объединения условий: союзом И или союзом ИЛИ соответственно.
Число, находящееся рядом с дугой (сплошной или пунктирной), указывает на определенность правила, а число рядом с условиями и заключениями - на определенность условий и заключений.
Лицо, принимающее решение, условиям (А, В, С), а также правилу присваивает коэффициент определенности от 0 до 1.
С помощью специальных формул рассчитывается коэффициент определенности для заключения.
Для простого правила, содержащего лишь одно условие, например, ЕСЛИ Е, ТО С, коэффициент определенности для заключения С рассчитывается так:
ct(C) = ct(E) · ct(правила)
где ct(C) - коэффициент определенности заключения С;
ct(E) - коэффициент определенности условия Е;
сt(правила) - коэффициент определенности правила.
 2014-02-02
2014-02-02 499
499







