(34) 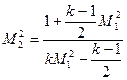 .
.
Коэффициент восстановления давления торможения 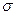 в функции от числа М
в функции от числа М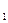 до скачка:
до скачка:
(35) 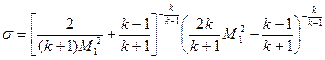
или в функции от числа 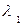 :
:
(36)  .
.
Коэффициент восстановления давления торможения выражается через приведенный секундный расход q (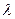 ):
):
(37) 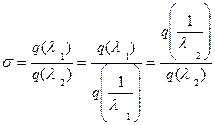 .
.
Скачок уплотнения может быть как прямым, так и косым (направлен под углом 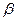 к обтекаемому телу) – рис.2. Косые скачки уплотнения возникают, например, при обтекании сверхзвуковым потоком клина с углом раствора
к обтекаемому телу) – рис.2. Косые скачки уплотнения возникают, например, при обтекании сверхзвуковым потоком клина с углом раствора 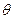 . Формулы для расчета параметров газа на косом скачке уплотнения следующие (38):
. Формулы для расчета параметров газа на косом скачке уплотнения следующие (38):
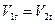 - касательные составляющие скоростей,
- касательные составляющие скоростей,
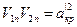 , где
, где 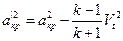
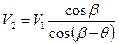 ,
,
 ,
,
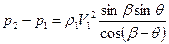
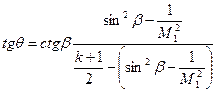

Рис.2. Возникновение скачка уплотнения при обтекании клина, заостренного и затупленного тела.
На рис.3. приведена зависимость угла поворота потока в косом скачке уплотнения 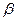 от угла раствора клина
от угла раствора клина 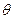 . Видно, что каждому заданному значению
. Видно, что каждому заданному значению 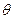 соответствует 2 значения угла
соответствует 2 значения угла 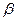 . Поэтому, теоретически может существовать две ударные волны. Большему значению
. Поэтому, теоретически может существовать две ударные волны. Большему значению 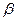 соответствует большее значение
соответствует большее значение 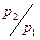 , а меньшему значению
, а меньшему значению 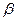 меньшее
меньшее 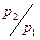 . Отношение
. Отношение 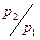 является мерой мощности скачка. Область выше линии
является мерой мощности скачка. Область выше линии 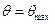 - это область сильных скачков, а область ниже данной линии – это область слабых скачков. На практике чаще встречаются случаи слабых скачков, т.к. они являются более устойчивыми.
- это область сильных скачков, а область ниже данной линии – это область слабых скачков. На практике чаще встречаются случаи слабых скачков, т.к. они являются более устойчивыми.
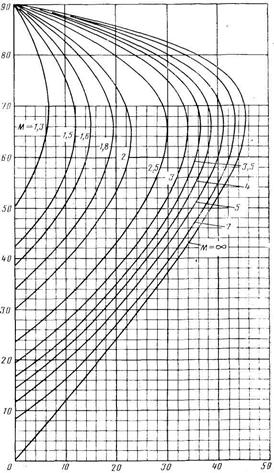
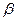
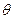
Рис.3. Зависимость 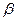 от
от 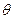 и
и 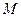 , при
, при 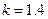 .
.
Кроме этого, для каждого числа 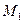 существует некоторое предельное значение угла
существует некоторое предельное значение угла 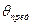 , такое что для
, такое что для 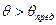 , решения уравнения (38.6) не существует. В этом случае косого скачка в виде присоединенной к вершине клина ударной волны не образуется. Образуется отошедшая ударная волна, располагающаяся на некотором расстоянии от тела. Если за косым присоединенным скачком уплотнения газ двигается с дозвуковой скоростью, то в случае отошедшей ударной волны за скачком существуют области дозвукового течения, линии критических значений скорости и области сверхзвукового течения.
, решения уравнения (38.6) не существует. В этом случае косого скачка в виде присоединенной к вершине клина ударной волны не образуется. Образуется отошедшая ударная волна, располагающаяся на некотором расстоянии от тела. Если за косым присоединенным скачком уплотнения газ двигается с дозвуковой скоростью, то в случае отошедшей ударной волны за скачком существуют области дозвукового течения, линии критических значений скорости и области сверхзвукового течения.
Пример возникновения ударной волны:
При обтекании сверхзвуковым газовым потоком твёрдого тела на его передней кромке образуется ударная волна, (иногда не одна, в зависимости от формы тела). На фото (рис.4) видны ударные волны, образованные на острие фюзеляжа модели, на передней и задней кромках крыла и на заднем окончании модели.
На фронте ударной волны, имеющем очень малую толщину (доли миллиметра), почти скачкообразно происходят кардинальные изменения свойств потока – его скорость относительно тела снижается и становится дозвуковой, давление в потоке и температура газа скачком возрастают. Часть кинетической энергии потока превращается во внутреннюю энергию газа. Все эти изменения тем больше, чем выше скорость сверхзвукового потока. При гиперзвуковых скоростях (10-30М) температура газа достигает нескольких тысяч градусов, что создаёт серьезные проблемы для аппаратов, движущихся с такими скоростями.

Рис.4. Фотография ударных волн при обтекании модели сверхзвуковым потоком в аэродинамической трубе. (Аэродинамическая лаборатория NASA).
Фронт ударной волны по мере удаления от аппарата постепенно принимает почти правильную коническую форму – рис.5., перепад давления на нём уменьшается с увеличением расстояния от вершины конуса, и ударная волна превращается в звуковую.
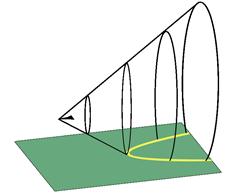
Рис.5. Распространение ударной волны, вызванной сверхзвуковым самолётом.
Жёлтая линия — след ударной волны на земле. Снаружи конуса ударной волны самолёт не слышен.
Когда эта волна достигает наблюдателя, находящегося, например, на Земле, он слышит громкий звук, похожий на взрыв. Распространенное заблуждение, будто бы это – следствие достижения самолётом в этот момент скорости звука, «преодоление звукового барьера». На самом деле это – прохождение мимо наблюдателя ударной волны, которая постоянно сопровождает самолёт, движущийся со сверхзвуковой скоростью. Обычно сразу после «хлопка» наблюдатель может слышать гул двигателей самолета, не слышный до прохождения ударной волны, поскольку самолёт приближался быстрее звуков, издаваемых им.
Движение вязкой жидкости.
Отличие гидродинамической модели реальной жидкости от идеальной жидкости состоит в том, что реальная жидкость обладает вязкостью и теплопроводностью. Вязкость жидкости приводит к появлению внутреннего трения, а теплопроводность – к термодинамической необратимости движения.
Вязкость
Вязкостью называется способность жидкостей и газов оказывать сопротивление изменению формы потока. Это внутренняя характеристика среды, которая зависит от свойств данной среды. Количественная мера вязкости среды – динамической и кинематической коэффициенты вязкости - 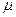 ,
,  . Тензор вязких напряжений в уравнении (4) в одномерном потоке запишется так:
. Тензор вязких напряжений в уравнении (4) в одномерном потоке запишется так:
(39) 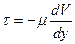 .
.
Данная формула называется законом Ньютона. Жидкости, для которых справедлива данная формула называются ньютоновскими, остальные называются неньютоновскими.
Коэффициент динамической вязкости 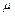 измеряется в
измеряется в 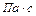 , кинематический коэффициент вязкости связан с динамическим следующим соотношением:
, кинематический коэффициент вязкости связан с динамическим следующим соотношением:
(40) 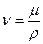
 .
.
Вязкость зависит также от температуры и давления потока, однако зависимость от давления достаточно слабая и ею часто пренебрегают. Зависимость вязкости от температуры для воды:
(41) 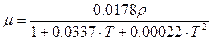 ,
,
где 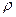 - плотность воды при температуре
- плотность воды при температуре 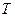 (при
(при 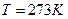 ,
, 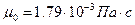 ).
).
Для газов и паров используется степенная формула:
(42) 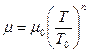 ,
,
где 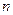 - показатель степени от 0.5 до 1 (для воздуха
- показатель степени от 0.5 до 1 (для воздуха 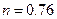 ,
, 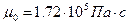 при
при 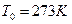 ).
).
Теплопроводность вязких жидкостей определяется законом Фурье:
(43) 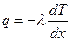 .
.
Режимы течений
Течения вязкой жидкости по характеру делятся на ламинарный и турбулентный режимы. Эти режимы характеризуются числом Рейнольдса
(44) 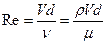 .
.
Ламинарный режим течения существует, когда число Рейнольдса данного течения меньше некоторого критического числа Рейнольдса 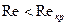 .
.
Критическое число Рейнольдса – это предельный режим течения, при котором еще сохраняется устойчивое ламинарное (слоистое) течение. Для различных видов течений критическое число Рейнольдса различное – 2300(для круглых труб), 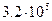 (для внешнего обтекания шара свободным потоком),
(для внешнего обтекания шара свободным потоком), 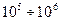 (для пограничного слое на тонкой пластины).
(для пограничного слое на тонкой пластины).

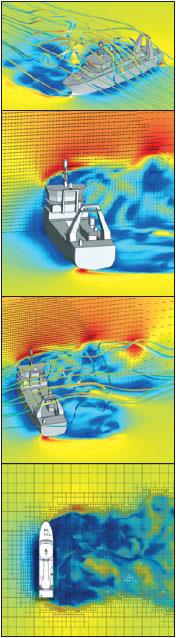
Рис.6. Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины.
В ламинарном потоке жидкости все параметры течения изменяются непрерывно, течение происходит слоями (меняются только две или одна компоненты вектора скорости), теплообмен между слоями жидкости происходит только за счет молекулярного движения теплового движения – рис.6.
В турбулентном потоке параметры течения изменяются хаотично, случайным образом (происходит изменение всех компонент вектора скорости). Перенос импульса в турбулентном потоке осуществляется не только за счет молекулярного движения, а главным образом за счет хаотичного движения отдельных объемов жидкости. Все параметры среды при турбулентном режиме течения можно представить в виде суммы двух составляющих – средней (характеризует основные свойства потока) и пульсационной (отклонение параметров потока от средних величин):
(45) 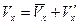 ,
, 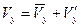 ,
, 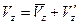 ,
, 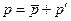 ,
, 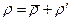 ,
, 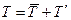 .
.
Пульсации основных параметров отличают ламинарный режим от турбулентного. Их наличие приводит к появлению в течении дополнительных напряжений, которые определяются формулой:
(46) 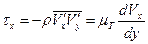 ,
,
где 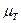 - коэффициент турбулентной вязкости.
- коэффициент турбулентной вязкости.
Система уравнений Навье-Стокса для вязкой жидкости
Для трехмерного нестационарного течения система уравнений Навье-Стокса запишется в виде (47):
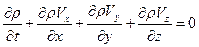
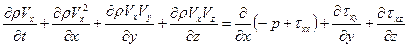 ;
;
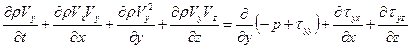 ;
;
 .
.
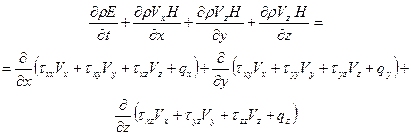 .
.
Дополнительные уравнения:
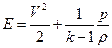 ,
, 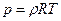 ,
, 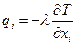 ,
, 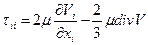 - добавочные нормальные напряжения, вызванные вязкостью жидкости,
- добавочные нормальные напряжения, вызванные вязкостью жидкости, 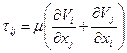 - касательные напряжения.
- касательные напряжения.
В приведенных выше формулах:
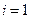 | 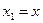 | 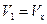 |
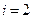 | 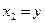 | 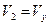 |
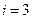 | 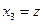 | 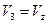 |
В этом случае система уравнений Навье-Стокса является замкнутой и может быть решена. Существует всего несколько точных решений уравнений Навье-Стокса. Все эти примеры основаны на упрощении исходной системы уравнений, после которых ее можно интегрировать. К таким задачам относятся – задача Пуазейля о ламинарном установившемся течении вязкой, несжимаемой жидкости в цилиндрической трубе. В этой задаче 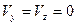 , а
, а 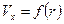 , где
, где 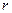 - радиус трубы.
- радиус трубы.
Из третьего и четвертого уравнений системы (47) получим, что
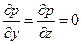 .
.
Из второго уравнения системы (47) найдем, что
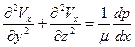 .
.
Интегрируя данное уравнение на участке трубы 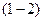 длиной
длиной 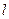 , получим
, получим
(48) 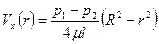 .
.
Таким образом, по радиусу трубы профиль скорости параболический. Данный профиль скорости называется профилем Пуазейля.
Объемный расход жидкости в таком случае будет рассчитываться по формуле:
(49) 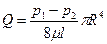 .
.
Другой частный случай решения системы уравнений Навье-Стокса – течение Куэтта. Ламинарное установившееся течение вязкой, несжимаемой жидкости между параллельными пластинами. В этом случае следуют данные формулы:
(50) 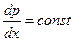 , а
, а 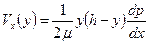 .
.
Другой пример – установившееся обтекание шара потоком вязкой несжимаемой жидкостью. Шар при движении не вращается. Течение ламинарное.
Общая сила сопротивления будет равна
(51) 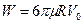 ,
,
где 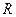 - радиус шара,
- радиус шара, 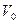 - скорость набегающего потока. Данная формула справедлива для чисел Рейнольдса меньше 1.
- скорость набегающего потока. Данная формула справедлива для чисел Рейнольдса меньше 1.
Коэффициент сопротивления равен
(52) 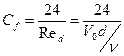 .
.
Течение жидкости в трубах.
Основной задачей течения вязкой жидкости в трубах является определение сопротивления трубопровода. Универсальная формула для определения сопротивления, пригодная для любого режима течения:
(53) 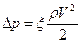 .
.
Однако в данной формуле, коэффициент сопротивления ξ – зависит не только от режима течения, но и от геометрических форм проточной части трубопровода. Аналогичного вида уравнение можно записать и для напряжения трения.
(54) 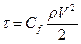 .
.
В последних двух уравнениях 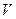 - средняя скорость потока.
- средняя скорость потока.
Используя уравнение (53) можно получить формулу для расчета падения давления по длине канала при равномерном движении потока, без местных сопротивлений
(55) 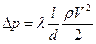 ,
,
где λ – коэффициент гидравлического сопротивления трубы.
Формула (55) отражает потери давления в результате трения.
Для различных режимов течений в трубах используются различные формулы расчета коэффициента сопротивления:

Для течения в плоском канале, высота h которого намного меньше его ширины коэффициент сопротивления запишется следующим образом:
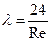 , при этом
, при этом 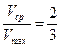 ,
, 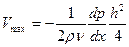 ,
, 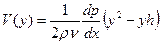 - профиль Пуазейля.
- профиль Пуазейля.
Для круглой трубы
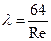 , при этом
, при этом 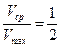 ,
, 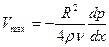 ,
, 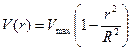 - профиль Пуазейля.
- профиль Пуазейля.
Для турбулентного стабилизированного течения в трубе справедливы следующие формулы:
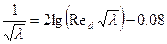 - ф. Прандтля,
- ф. Прандтля, 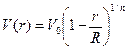 , где n зависит от числа Рейнольдса. Если число Рейнольдса равно 107, то n=4.
, где n зависит от числа Рейнольдса. Если число Рейнольдса равно 107, то n=4. 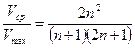 .
.
На коэффициент сопротивления 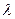 влияет не только режим течения и скорость потока, но и форма труб. В трубах некруглого сечения поперечная составляющая вектора скорости не равна 0 и в трубе возникают вторичные течения – движение жидкости в поперечном направлении. Данный вид течений возникает только в турбулентном потоке. Вторичные течения приводят к тому, что скорость в углах труб становится выше, чем в других ее участках. Имеют особенности также течения в криволинейных трубах. Главная особенность здесь – наличие центробежной силы, которая оттесняет поток к внешней поверхности трубы. Кроме того в таких трубах также возникают вторичные течения. Для оценки влияния кривизны трубы на коэффициент сопротивления вводится критерий Дина:
влияет не только режим течения и скорость потока, но и форма труб. В трубах некруглого сечения поперечная составляющая вектора скорости не равна 0 и в трубе возникают вторичные течения – движение жидкости в поперечном направлении. Данный вид течений возникает только в турбулентном потоке. Вторичные течения приводят к тому, что скорость в углах труб становится выше, чем в других ее участках. Имеют особенности также течения в криволинейных трубах. Главная особенность здесь – наличие центробежной силы, которая оттесняет поток к внешней поверхности трубы. Кроме того в таких трубах также возникают вторичные течения. Для оценки влияния кривизны трубы на коэффициент сопротивления вводится критерий Дина:
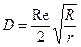 ,
,
где 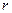 - радиус кривизны.
- радиус кривизны.
Для ламинарных течений
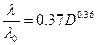 .
.
Для турбулентных
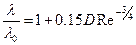 .
.
Кроме этого сопротивление трубопровода зависит от наличия местных сопротивлений, которые в большинстве случаев меняют форму потока жидкости – задвижки, вентили, колена, диафрагмы и т.д. В этом случае формула (55) изменится следующим образом:
(56) 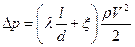 ,
,
где 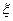 - коэффициент местного сопротивления, зависящий от вида сопротивления:
- коэффициент местного сопротивления, зависящий от вида сопротивления:
| № п/п | Местное гидравлическое сопротивление | Ориентировочное значение коэффициента ξ |
| Вход в трубу из емкости | 0,5 | |
| Внезапное сужение с диаметра d на диаметр dmin | 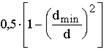 | |
| Внезапное расширение с диаметра d на диаметр dmax | 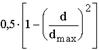 | |
| Диафрагма в прямой трубе диаметром d; d0 - диаметр отверстия в диафрагме: (d/d0) = 0,3 | ||
| 0,4 | ||
| 0,5 | ||
| 0,6 | ||
| 0,8 | 0,5 | |
| Диффузор при переходе с диаметра d0 на диаметр d при его длине L и угле расширения a; d > d0 | 0,25 | |
| Конфузор длиной L и с углом сужения a; d > d0 | 0,1 | |
| Отводы крутоизогнутые и плавные при угле поворота a и радиусом поворота R, в том числе: | ||
| отводы плавные при угле поворота 900 | 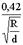 | |
| отводы плавные стандартные при R/d = 1,5 и угле поворота 900 | 0,34 | |
| Отводы стальные секционные | до 0,4 | |
| Колено с острой кромкой и углом поворота 900: | ||
| при одинаковых диаметрах без ниши | 1,65 | |
| то же, с нишей | 2,0 | |
| при переходе на меньший диаметр без ниши | 2,8 | |
| то же, с нишей | 3,5 | |
| Z-образное колено (из двух колен с углом поворота потока в колене на 30 0) | 0,32 | |
| Тройник: | ||
| проход | 0,35 | |
| боковое ответвление | 1,5 | |
| при симметричном разделении потока | 2,5 | |
| Крестовина: | ||
| боковое ответвление | 3,0 | |
| проход | 2,0 | |
| Задвижка: | ||
| клиновая, полностью открытая | 0,15 | |
| шиберная, полностью открытая | 0,05 | |
| Вентиль при полном открытии: | ||
| стандартный | 4 - 6 | |
| штампованный | 7,8 | |
| угловой | 2,3 | |
| прямоточный | 1,3 | |
| Клапан обратный: | ||
| поворотный | 2,0 | |
| подъемный | 8,0 | |
| Кран | 3,0 | |
| Компенсатор: | ||
| линзовый | 0,3 | |
| сальниковый | 0,5 | |
| П-образный | 2,0 | |
| волнистый d = 0,1 - 0,3 м | 0,4 | |
| 0,3 -0,5 м | 0,3 | |
| свыше 0,5 м | 0,02 | |
| Выход из трубы в емкость: | ||
| для турбулентного потока | 1,0 | |
| для ламинарного потока | 2,0 |
Потери напора в трубопроводе можно рассчитать по следующей формуле:
(57) 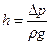 .
.
Теория пограничного слоя.
Широко разработанная теория движения идеальных жидкостей дает вполне удовлетворительную картину действительных течений, за исключением областей, расположенных вблизи поверхностей обтекаемых тел. Здесь существенное значение приобретают силы внутреннего трения или силы вязкости, которые являются определяющими в возникновении сопротивления тел при движении в жидкости. Пренебрежение этими силами приводят к тому, что сопротивление тела оказывается равным 0, что противоречит опытным данным. Экспериментально установлено, что влияние вязкости наиболее существенно в тонком слое жидкости, прилегающем к поверхности тела. Этот слой имеет малую толщину по сравнению с длиной тела и называется пограничным слоем. Теория, изучающая поведение жидкости в пограничном слое получила название теории пограничного слоя.
Уравнения пограничного слоя (уравнения Прандтля) для несжимаемой вязкой жидкости имеют следующий вид (58):
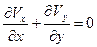
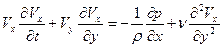 ;
;
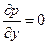 .
.
Естественно, что пограничные слои в ламинарном и турбулентном потоках различны. Т.к. в ламинарном потоке скорости не очень высоки, то и влияние сил вязкости сказывается на них сильнее. В турбулентном же потоке, скорости движения жидкости могут быть очень большими, то влияние вязких сил слабее.
Основные параметры, характеризующие пограничный слой:
Толщина пограничного слоя 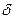 , толщина вытеснения
, толщина вытеснения 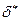 , толщина потери импульса
, толщина потери импульса 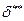 .
.
Для ламинарного пограничного слоя (59)
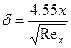 ,
, 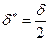 ,
, 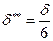 ,
, 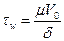 ,
, 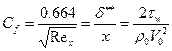 ,
, 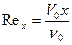 , параметры с 0 – параметры набегающего потока,
, параметры с 0 – параметры набегающего потока, 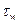 - напряжение трения на стенке. Распределение скорости подчиняется закону Пуазейля.
- напряжение трения на стенке. Распределение скорости подчиняется закону Пуазейля.
Основное уравнение, связывающее основные характеристики пограничного слоя – интегральное уравнение импульсов или уравнение Кармана:
(60) 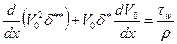
Для турбулентного пограничного слоя (61)
 ,
, 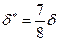 ,
, 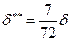 ,
, 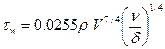 ,
, 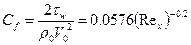 .
.
Интегральное уравнение импульсов:
(62) 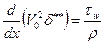
Одной из особенностей пограничного слоя является явление отрыва, которое возникает при наличии в потоке положительного перепада давлений 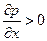 , например при обтекании профилей различной формы, при течении газа в диффузорах.
, например при обтекании профилей различной формы, при течении газа в диффузорах.

Рис.7. Отрыв пограничного слоя.
При расширении области поток замедляется, а давление возрастает. В результате растет влияние сил вязкости и трения. Энергии частиц около обтекаемой поверхности не хватает на преодоление этих возросших сил и в некоторой точке частицы потока останавливаются. Вышележащие слои жидкости, обтекая остановившиеся частицы, начинают двигаться в обратном направлении – в потоке возникает возвратное движение жидкости. Возвратно движущиеся частицы, встречаясь с основным потоком, оттесняют пограничный слой от стенки. В результате, происходит резкий рост толщины пограничного слоя, что может привести к существенному изменению основного внешнего течения, которое в этом случае становится существенно зависимым от свойств вязкости среды. Отрыв потока относится к числу вредных явлений, вызывающих резкое повышение сопротивления обтекаемых жидкостью тел, опасные их вибрации, а в случае течения жидкости по трубам и каналам к уменьшению полезного расхода жидкости, возрастанию потерь энергии и уменьшению коэффициента полезного действия.
Тепловые и диффузионные потоки в пограничном слое. Тройная аналогия Рейнольдса.
Рассмотрим следующие величины, имеющие особое значение при расчете пограничного слоя на пластине:
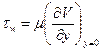 - напряжение трения на стенке,
- напряжение трения на стенке,
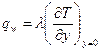 - тепловой поток на стенке,
- тепловой поток на стенке,
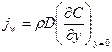 - диффузионный поток на стенке (
- диффузионный поток на стенке (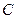 - концентрация вещества,
- концентрация вещества, 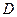 - коэффициент диффузии).
- коэффициент диффузии).
Зная напряжение трения на стенке можно рассчитать коэффициент сопротивления пластины: 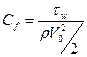 . Зная тепловой поток на стенке можно вычислить тепловое число Стантона, которое характеризует, какая доля общего тепла в ядре потока попадет на стенку:
. Зная тепловой поток на стенке можно вычислить тепловое число Стантона, которое характеризует, какая доля общего тепла в ядре потока попадет на стенку: 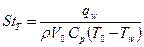 (
(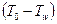 - разность температур в ядре потока и на стенке). Аналогично тепловому числу Стантона можно рассмотреть диффузионное число Стантона
- разность температур в ядре потока и на стенке). Аналогично тепловому числу Стантона можно рассмотреть диффузионное число Стантона 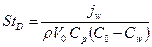 .
.
Согласно тройной аналогии Рейнольдса
(63) 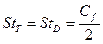 .
.
Данная формула справедлива как для ламинарного режима течений, так и для турбулентного.
Приближенное решение системы уравнений Навье-Стокса
Аналитическому решению они не поддаются, однако проектировать подводные лодки и особенно самолеты все-таки нужно. Практики решают уравнения приближенно. И здесь, конечно, используются на полную мощь компьютерные технологии. За последние десяток лет возник целый раздел на грани математической физики и вычислительной динамики жидкостей и газов (computational fluid dynamics, CFD).
В настоящее время существует множество программных продуктов (как коммерческих, так и свободных), реализующих различные задачи вычислительной динамики –FLUENT, CFX, StarCD, FlowVision и многие другие.
Задачи
1. Трубка Пито помещена в поток жидкости, движущейся в открытом канале. Жидкость поднялась в насадке на высоту 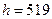 мм. Определить скорость движения жидкости, если давление потока составляет 1.294 атм. Плотность жидкости 1000
мм. Определить скорость движения жидкости, если давление потока составляет 1.294 атм. Плотность жидкости 1000 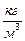 , ускорение свободного падения
, ускорение свободного падения 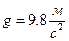 .
.
2. Местная звуковая скорость на крыле самолета наступает при числе 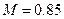 . С какой максимальной скоростью может лететь самолет на высоте 8000м, не превышая критической скорости полета? Определить температуру потока, при которой местная скорость равна скорости звука.
. С какой максимальной скоростью может лететь самолет на высоте 8000м, не превышая критической скорости полета? Определить температуру потока, при которой местная скорость равна скорости звука.
3. Самолет летит на высоте 5000м. Давление заторможенного потока равно 684 мм. рт. ст. Какова скорость самолета и на сколько ее надо увеличить, чтобы лететь со скоростью, равной скорости звука на этой высоте.
4. Температура газа в камере сгорания двигателя 2800 К, газовая постоянная 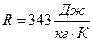 , показатель адиабаты
, показатель адиабаты 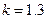 . Определить критическую скорость звука и скорость звука заторможенного газа.
. Определить критическую скорость звука и скорость звука заторможенного газа.
5. Определить размеры критического и выходного сечений сопла Лаваля и параметры заторможенного потока перед соплом для получения воздушного потока с числом 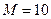 , давлением в выходном сечении сопла
, давлением в выходном сечении сопла 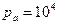 Па и температурой потока
Па и температурой потока  К при расходе воздуха через сопло
К при расходе воздуха через сопло 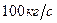 . Принять
. Принять 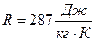 ,
, 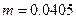 ,
, 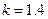 .
.
6. Продукты сгорания вытекают через сопло Лаваля с числом 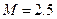 во внешнюю среду, где давление
во внешнюю среду, где давление  (
(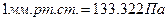 ). Температура потока в выходном сечении сопла равна
). Температура потока в выходном сечении сопла равна 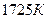 . Определить параметры газа в камере двигателя (
. Определить параметры газа в камере двигателя (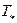 ,
, 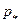 ,
,  ), если истечение расчетное, показатель адиабаты продуктов сгорания
), если истечение расчетное, показатель адиабаты продуктов сгорания 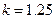 , а газовая постоянная
, а газовая постоянная 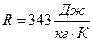 .
.
7. Плоская пластина, находящаяся под некоторым углом атаки, обдувается сверхзвуковым потоком воздуха с числом 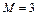 (
(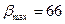 ). При каком угле атаки
). При каком угле атаки 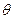 косой скачок уплотнения превратится в отошедшую криволинейную ударную волну?
косой скачок уплотнения превратится в отошедшую криволинейную ударную волну?
8. Рассчитать параметры газа (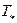 ,
, 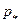 ,
,  ) в камере сопла Лаваля с
) в камере сопла Лаваля с 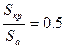 , если сопло работает в расчетном режиме, а воздух вытекает из сопла в среду с давлением 760 мм. рт. ст.
, если сопло работает в расчетном режиме, а воздух вытекает из сопла в среду с давлением 760 мм. рт. ст.
9. Стальной шарик диаметром 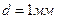 , падает с постоянной скоростью
, падает с постоянной скоростью 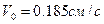 в большом сосуде, наполненном касторовым маслом (
в большом сосуде, наполненном касторовым маслом (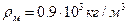 ). Найти динамическую вязкость касторового масла.
). Найти динамическую вязкость касторового масла.
10. Углекислый газ течет по трубе со скоростью 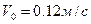 . Диаметр трубы
. Диаметр трубы 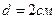 . Какому режиму движения соответствует течение газа по трубе, если его кинематическая вязкость равна
. Какому режиму движения соответствует течение газа по трубе, если его кинематическая вязкость равна 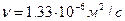 .
.
11. Подсчитайте максимальный расход керосина (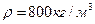 ,
,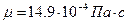 ) через трубу диаметром 24мм при сохранении ламинарного режима течения. Критическое число Рейнольдса определять по скорости на оси трубы.
) через трубу диаметром 24мм при сохранении ламинарного режима течения. Критическое число Рейнольдса определять по скорости на оси трубы.
12. Определить касательное напряжение на стенке трубы с диаметром 3.5 мм при течении по ней этилового спирта 92%-й концентрации с температурой 293К (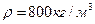 ,
,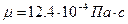 ), если расход спирта при этом 0.2л/мин. Определить режим течения по скорости на оси трубы.
), если расход спирта при этом 0.2л/мин. Определить режим течения по скорости на оси трубы.
13. Определить касательное напряжение на стенках канала, образованного параллельными неподвижными пластинами, отстоящими одна от другой на расстоянии 0.5мм при движении между ними жидкости с расходом 2см2/с на 1м ширины канала и с вязкостью 0.045Па·с.
14. Для создания прибора по определению вязкости нефтепродуктов методом падающего шарика необходимо определить максимальный диаметр шарика, изготовленного из алюминия. Опыт должен проходить при числе Рейнольдса не более 0.6, примерное значение коэффициента вязкости нефтепродукта 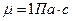 , а плотность
, а плотность 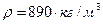 .
.
15. По трубопроводу диаметром 150мм перекачивается вода с расходом 60л/с. На длине трубопровода был замерен с помощью ртутно-водяного манометра перепад давлений, который оказался равным 89мм. Определить коэффициент сопротивления трубопровода.
16. Вычислить потерю напора, вызванную внезапным расширением трубопровода от 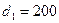 мм до
мм до  мм, если по трубопроводу прокачивается 0.2 м3/с воды при температуре 293К. на сколько уменьшатся потери напора, если участки трубы соединить коническим диффузором с центральным углом раствора 60?
мм, если по трубопроводу прокачивается 0.2 м3/с воды при температуре 293К. на сколько уменьшатся потери напора, если участки трубы соединить коническим диффузором с центральным углом раствора 60?
 2014-02-02
2014-02-02 2270
2270






