Нормальное распределение. Рассмотрим Пример 2, в котором случайная величина Х представлена выборкой {хi}

Рассмотрим Пример 2, в котором случайная величина Х представлена выборкой {х_i}. Эти данные получены оператором при измерении свойства А с помощью СИ. Значение А является постоянным. Случайные возмущения на входе и выходе СИ привели к тому, что (x_j) рассеяны в диапазоне D = x_max - x_min _., при этом случайные значения Х является распределенными по нормальному закону

Х 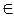N (σ², A),

где σ² = D – дисперсия, А – математическое ожидание случайной величины.

Используется и другие названия для этих параметров:

σ – среднее квадратическое отклонение, СКО,

А – среднее значение или действительное значение величины Х.

В теории вероятностей принято, что Х является заданной, если являются известными:

а) представительная выборка { х_i } и

б) локальные вероятности { Р _i}.

Как задаются или рассчитываются { Р _i}?

Для этого используют, например, характеристику №2 – плотность вероятности ƒ(х), которая имеет вид

f (x) = 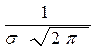. (10)

В (10) множитель, , называется амплитудой.

Форма f (x) напоминает «Шляпу» для условий Задачи 2 (Рис. 5)

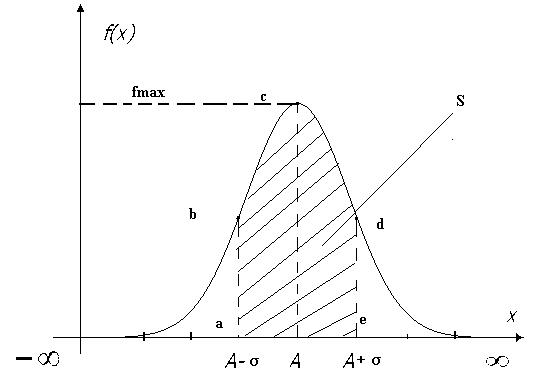
Рис. 4.

Плотность вероятности f (x) для Х 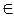N (σ²,A)

Отметим свойства f(x):

1) f(x) является симметричной относительно оси, проходящей через х=А. Причина этого заключается в том, что аргумент является квадратичной формой (x-A)²,

2) f(x) имеет максимум f _max при х=А (точка c), при х=А (проверить самостоятельно),

3) f(x) имеет 2 точки перегиба (точки b и d): при х = А - σ и при х = А+σ (проверить самостоятельно), то есть в этих точках

=0,

4) f(x) является отличной от нуля на периферии, и только в пределе она уменьшается до нуля

lim f(x) = 0,

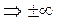
5) численное значение интеграла и соответствующая площадь S под «Шляпой» составляют

S = I = dx = 1.

Плотность вероятности для статистики Z

Набор случайных величин Х = { х_i } рассматривается как статистика № 1.

Делаем замену: переходим к случайной величине и исследуем статистику №2 – случайную переменную Z = { z_i }. Она имеет обобщенный вид по сравнению со статистикой №1 и применяется для обработки случайных опытных данных.

Примем, что σ = 1 и А = 0, тогда x = Z. Плотность вероятности можно записать в форме

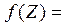
. (11)

Случайная величина Z относится к нормально распределенным величинам Z 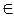N (1, 0). Форма f (Z) напоминает «Шляпу» для условий Задачи 1 (Рис. 5)

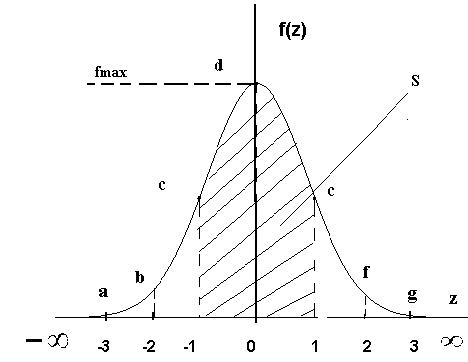
Рис. 5. Плотность вероятности f (Z)

Свойства плотности вероятности f(Z)

а) 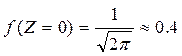, f(Z) является симметричной относительно нуля, имеет максимум при z = 0.

б) Границы погрешности определяются с помощью интегрирования

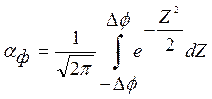. (12)

Доверительные интервалы можно изобразить в виде соответствующей площади. Например, для z являются распространенными следующие границы: доверительные интервалы и вероятности составляют

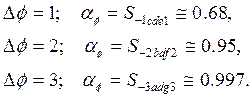
Уровень значимости, q = 1 – α, составляет q = 0.3 при выбранном Δ _ф = 3, для площадей на периферии справедливо

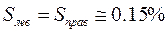В предельном случае

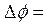
. (13)

Из математики известно, что интеграл Пуассона I имеет следующее значение

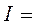
. (14)

Существуют таблицы для (Табл. П-1, Рабинович C.Г. Погрешности измерений), которые используются для вычисления характеристик случайных величин, подчиняющихся распределению Z 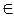N (1, 0).