Случай функции трех и более числа переменных

В том случае, когда следует найти локальные экстремумы функции 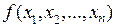, следует сначала отыскать все критические точки функции, решив систему из 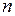уравнений с 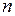переменными: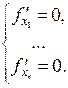

Для того, чтобы выяснить, будет ли критическая точка 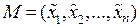точкой локального экстремума, следует сосчитать в этой точке все частные производные второго порядка, составить матрицу вида 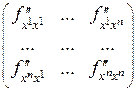и рассмотреть последовательность определителей, состоящих из элементов в левом верхнем углу матрицы: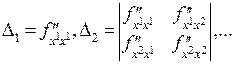

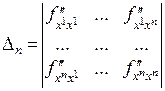. Минимум в критической точке 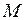будет тогда и только тогда, когда 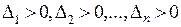. Максимум в критической точке 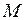будет тогда и только тогда, когда 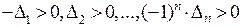, то есть, знаки у последовательности определителей обязаны чередоваться.