2014-02-02
3617
Пусть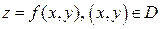 
, – функция двух переменных. Графическим изображением этой функции является поверхность над областью 
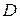. Рассмотрим точку 
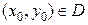, в которой данная функция имеет конечные частные производные 
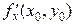и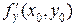 
.
Пересечением плоскости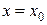 
с заданной поверхностью является кривая. Аппликата этой кривой определяется по формуле 
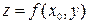. Частная производная 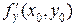является тангенсом угла наклона касательной к полученной кривой , лежащей в плоскости 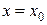, с положительным направлением оси OY в точке 
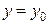. Направляющий вектор этой касательной имеет координаты 
.
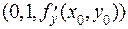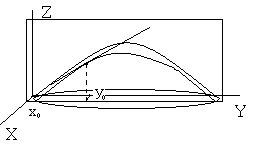
Пересечением плоскости 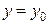с заданной поверхностью является кривая. Аппликата этой кривой определяется по формуле 
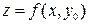. Частная производная 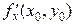является тангенсом угла наклона касательной к полученной кривой 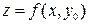, лежащей в плоскости 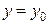, с положительным направлением оси OX в точке 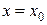. Направляющий вектор этой касательной имеет координаты 
.
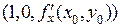При исследовании функций нескольких переменных приходится брать производные высших порядков по различным переменным. Например, символ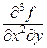 
означает, что у функции взята производная по переменной 
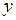и от нее – дважды производная по 
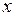. Эта же производная может быть записана как 
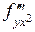. Такие производные можно также брать с применением пакета программ MAXIMA. При дифференцировании функции по нескольким переменным используется команда diff, за ней в скобках записывается функция, а дальше через запятые все переменные, по которым берутся производные, и после каждой переменной – через запятую– порядок производной. Например, мы хотим взять производную 
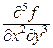, где 
. Мы вводим команду diff(sin(x^2+3*y),x,2,y,3), нажимаем клавиши Shift+Enter и получаем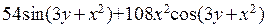 
.
Необходимое условие локального экстремума.
Теорема о необходимом условии экстремума дифференцируемой функции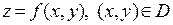 
. Необходимым условием существования экстремума дифференцируемой в точке 
функции является система равенств
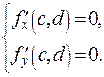
П р и м е р. Найти локальный экстремум функции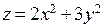 
, заданной на всей плоскости XOY.
Запишем необходимое условие экстремума данной функции: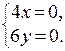
Отсюда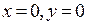 
. Следовательно, координаты критической точки, то есть точки, в которой частные производные первого порядка одновременно обращаются в ноль, (0,0).
Построим график функции в окрестности начала координат и проверим, действительно ли точка (0,0) является точкой локального экстремума. Введем команду plot3d(2*x^2+3*y^2,[x,-2,2],[y,-2,2]) нажмем клавиши Shift+Enter. Мы получим следующую картину.
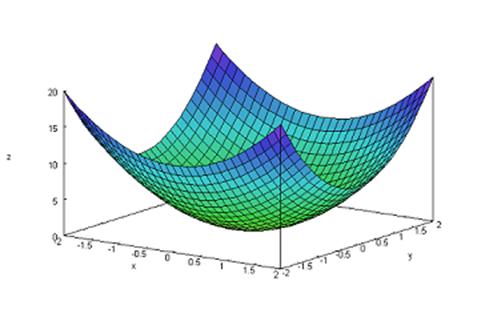
Очевидно, что в точке (0,0) локальный минимум.
Выполнение необходимого условия экстремума не обязательно обеспечивает действительное наличие экстремума в точке, то есть, критическая точка функции может не быть точкой локального экстремума. В качестве примера рассмотрим функцию двух переменных 
. Критической точкой для этой функции является точка (0,0). Однако эта точка является не экстремальной, а седловой.
hypar.wxm
