Взаимосвязь теории отношения предпочтения-безразличия
Лекция 5. Теория отношения предпочтения-безразличия
Если потребитель предпочитает набор 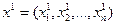 потребительскому набору
потребительскому набору 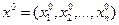 и из этих наборов обязательно выберет набор
и из этих наборов обязательно выберет набор 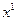 , то говорят, что на потребительских наборах
, то говорят, что на потребительских наборах 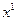 и
и  задано отношение сильного предпочтения или
задано отношение сильного предпочтения или 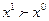 . Отношение предпочтения не обладает свойством рефлексивности
. Отношение предпочтения не обладает свойством рефлексивности 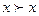 .
.
Если потребителю все равно, какой из двух наборов выбирать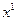 или
или  , то говорят, что на потребительских наборах
, то говорят, что на потребительских наборах 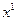 и
и  задано отношение безразличия, т.е.
задано отношение безразличия, т.е. 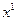 ̴
̴  . Отношение безразличия есть отношение эквивалентности, обладающее свойством рефлексивности
. Отношение безразличия есть отношение эквивалентности, обладающее свойством рефлексивности 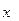 ̴
̴ 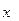 , симметричности
, симметричности  ̴
̴ 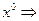
 ̴
̴  и транзитивности
и транзитивности  ̴
̴ 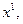
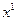 ̴
̴ 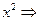
 ̴
̴ 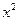 .
.
Если потребительский набор 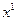 предпочитается или безразличен для набора
предпочитается или безразличен для набора  , то говорят, что на потребительских наборах
, то говорят, что на потребительских наборах 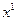 и
и  задано отношение предпочтения-безразличия, т.е. (
задано отношение предпочтения-безразличия, т.е. (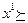
 ). Отношение предпочтения-безразличия представляет собой отношение порядка, т.е. такое бинарное отношение, которое обладает свойствами рефлексивности
). Отношение предпочтения-безразличия представляет собой отношение порядка, т.е. такое бинарное отношение, которое обладает свойствами рефлексивности  , антисимметричности
, антисимметричности 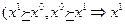 ̴
̴ 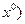 , транзитивности
, транзитивности 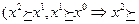
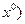 . Функция полезности задает отношение предпочтения-безразличия следующим образом:
. Функция полезности задает отношение предпочтения-безразличия следующим образом:  . Или
. Или 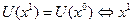 ̴
̴  ,
, 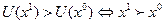 .
.
Карта линий безразличия задает отношение предпочтения-безразличия следующим образом: если потребительский набор 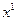 находится на линии безразличия
находится на линии безразличия 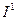 , расположенной выше и правее линии
, расположенной выше и правее линии 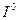 , на которой находится набор
, на которой находится набор  , то
, то 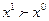 . Если наборы находятся на одной кривой безразличия, то
. Если наборы находятся на одной кривой безразличия, то 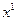 ̴
̴  . Имеется отношение предпочтения-безразличия, так называемое лексикографическое упорядочение, для которого не существует функции полезности. Таким образом, кроме количественной и порядковой теории полезности теория отношения предпочтения-безразличия представляет собой более общую теорию потребительского поведения.
. Имеется отношение предпочтения-безразличия, так называемое лексикографическое упорядочение, для которого не существует функции полезности. Таким образом, кроме количественной и порядковой теории полезности теория отношения предпочтения-безразличия представляет собой более общую теорию потребительского поведения.
Отношение предпочтения-безразличия обладает свойством полноты. Свойство полноты означает, что множество всех потребительских наборов таких, что 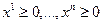 , является вполне упорядоченным множеством по отношению предпочтения-безразличия
, является вполне упорядоченным множеством по отношению предпочтения-безразличия 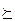 . По отношению
. По отношению 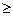 , которое для
, которое для 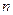 -мерных векторов понимается как покоординатное, множество потребительских наборов является только частично упорядоченным множеством.
-мерных векторов понимается как покоординатное, множество потребительских наборов является только частично упорядоченным множеством.
Множество 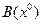 всех потребительских наборов
всех потребительских наборов 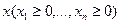 , предпочитаемых или безразличных набору
, предпочитаемых или безразличных набору  , называется хорошим множеством для набора
, называется хорошим множеством для набора  , т.е.
, т.е. 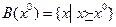 .
.
Множество 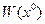 всех потребительских наборов
всех потребительских наборов  , которым набор
, которым набор  предпочитается или безразличен, называется плохим множеством для набора
предпочитается или безразличен, называется плохим множеством для набора  , т.е.
, т.е.  .
.
Множество 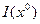 всех потребительских наборов
всех потребительских наборов 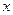 , безразличных набору
, безразличных набору  , называется множеством безразличия для набора
, называется множеством безразличия для набора  , т.е.
, т.е.  ̴
̴ 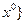 .
.
Неравенство 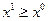 для
для 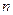 -мерных векторов
-мерных векторов 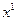 и
и  понимается покоординатно
понимается покоординатно 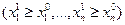 , неравенство
, неравенство 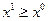 означает, что справедливо неравенство
означает, что справедливо неравенство 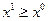 и хотя бы для одной координаты
и хотя бы для одной координаты 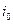 справедливо строгое неравенство
справедливо строгое неравенство  .
.
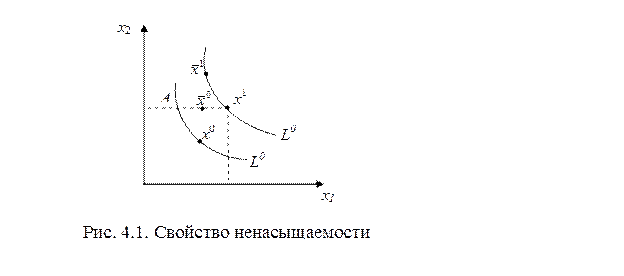
Свойство ненасыщаемости означает, что из 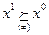 следует, что
следует, что 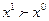 , рис. 4.1. Обратное
, рис. 4.1. Обратное 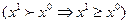 , очевидно, не имеет места. На рис. 4.1.
, очевидно, не имеет места. На рис. 4.1. 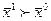 , однако неверно, что
, однако неверно, что 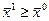 , ибо для них
, ибо для них 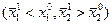 . Свойство ненасыщаемости справедливо не всегда (кривые безразличия в таком случае напоминают классическую кривую предложения с положительным наклоном).
. Свойство ненасыщаемости справедливо не всегда (кривые безразличия в таком случае напоминают классическую кривую предложения с положительным наклоном).
 Отношение предпочтения-безразличия обладает свойством непрерывности множеств безразличия
Отношение предпочтения-безразличия обладает свойством непрерывности множеств безразличия 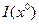 , строгой выпуклости для любого потребительского набора, гладкости функции полезности, если функция полезности включается в рассмотрение.
, строгой выпуклости для любого потребительского набора, гладкости функции полезности, если функция полезности включается в рассмотрение.
Отношение на множестве потребительских наборов называется отношением предпочтения-безразличия, если для него характерны восемь свойств: рефлексивности, антисимметричности, транзитивности, полноты, ненасыщаемости, непрерывности, строгой выпуклости и гладкости функции полезности.
Отношение предпочтения-безразличия и функция полезности. Отношение предпочтения-безразличия, для которого выполняются названные выше свойства, кроме строгой выпуклости и гладкости функции полезности, однозначно определяет функцию полезности 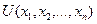 . В случае
. В случае 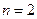 в каждой точке кривой безразличия функция полезности принимает конкретное значение. Поэтому
в каждой точке кривой безразличия функция полезности принимает конкретное значение. Поэтому 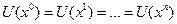 и множество значений полезности непрерывно. Непрерывность означает, что если
и множество значений полезности непрерывно. Непрерывность означает, что если 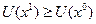 , то
, то  ; или наоборот, если
; или наоборот, если  , то
, то 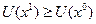 . Доказательство не приводится.
. Доказательство не приводится.
Лексикографическое упорядочение 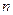 -мерных векторов аналогично упорядочению студентов группы по алфавиту: Александров, Белоусов, Васильев и т.д. Если
-мерных векторов аналогично упорядочению студентов группы по алфавиту: Александров, Белоусов, Васильев и т.д. Если 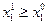 , то вектор
, то вектор 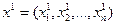 лексикографически предпочитается вектору
лексикографически предпочитается вектору 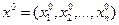 , что записывается так:
, что записывается так: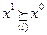 . Если
. Если 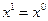 и
и 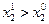 ,то
,то 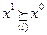 и т.д.
и т.д.
Лексикографическое упорядочение обладает свойствами рефлексивности, антисимметричности, транзитивности, полноты, ненасыщаемости. Однако оно не удовлетворяет предположению о непрерывности. Это утверждение приводится без доказательства. Для лексикографического упорядочения не существует функции полезности. Положение приводится без доказательства.
 2014-02-02
2014-02-02 743
743








