2014-02-02
628
Предельный расход по полезности и предельный расход по цене продукта (лемма Шепарда).
Предельный расход по полезности равен множителю Лагранжа:
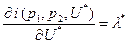(1.24)
Пусть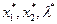 
есть решение задачи 
→
,
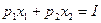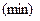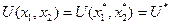на условный экстремум. Тогда имеем тождества
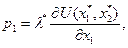(1.25)
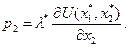
Равенство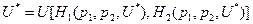 
является тождеством по 
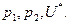Продифференцируем последнее выражение по 
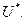Получим
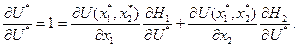(1.26)
Продифференцируем функцию расходов по максимальной полезности. 
В преобразованиях использовалась подстановку значений цен из (1.25) и (1.26). Утверждение (1.24) доказано.
Полученный вывод позволяет оценить новый минимальный уровень расхода потребителя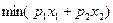 
, который получим при относительно малом изменении максимально возможной общей полезности на 
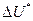, т.е. при 
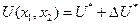. Он приблизительно равен 
при 
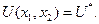Приближенное равенство означает, что при увеличении уровня полезности, например, на одну единицу, потребителю необходимо существенно увеличить расход.
Лемма Шепарда о предельном расходе по цене продукта утверждает, что предельный расход по цене одного из продуктов равен объему этого продукта в оптимальном наборе.
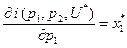(1.27)
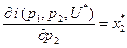
Продифференцируем равенство 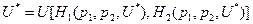по переменной цене. Получим выражение предельной полезности по цене продукта:
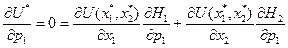. (1.28)
Имеем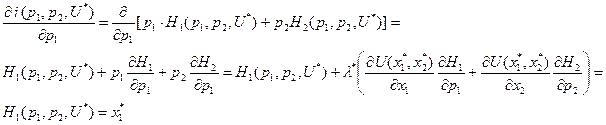 
В преобразованиях использованы подстановки: необходимое условие максимума функции Лагранжа(1.25) и предельная полезность по цене продукта (1.28).
Выражение для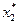 
доказывается аналогично.
Выражение цен в равенстве (1.25) позволяет оценить новый минимум расхода 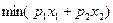, который при относительно малом изменении цены, например 
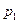, имеет вид: 
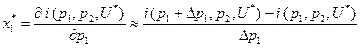. Отсюда следует 
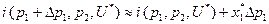. Минимальное значение 
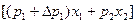при 
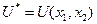приблизительно равно минимальному значению 
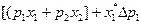при .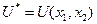
Для любого условия (1.4.4) имеют вид: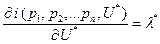 
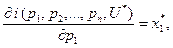
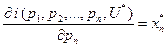
Взаимосвязь между решением задач максимизации функции полезности и минимизации расходов представлена ниже.
| Задача максимизации функции полезности имеет вид: | Задача минимизации расходов |
| 
|
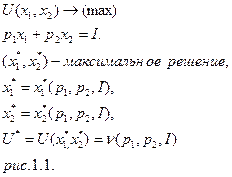
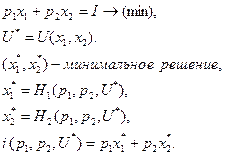
Используем решения задач максимизации функции полезности и минимизации расходов для вывода уравнения Е. Слуцкого и для представления его в коэффициентах эластичности.
