Рациональные корни

Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.

Если многочлен f (x) степени n приводим, то один из множителей имеет степень не выше n /2. Обозначим этот множитель через g (x). Поскольку все коэффициенты многочленов суть целые числа, то для любого целого a значение f (a) делится без остатка на g (a). Выберем m= 1+ n /2 различных целых чисел a _i, i =1,…, m. Для чисел g (a _i) существует конечное число возможностей (число делителей любого ненулевого числа конечно), а следовательно, существует конечное число многочленов, которые могут быть делителями f (x). Осуществив полный перебор, либо покажем неприводимость многочлена, либо разложим его в произведение двух многочленов. К каждому множителю применим указанную схему до тех пор, пока все множители не станут неприводимыми многочленами.

Пусть 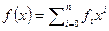- многочлен с целыми коэффициентами и содержанием 1, и, 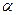- его рациональный корень. Представим этот корень в виде несократимой дроби 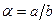. Многочлен f(x) представляется в виде произведения примитивных многочленов 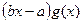. Следовательно, числитель a является делителем 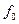, а знаменатель – делителем 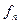. Более того, для любого целого k значение f(k) делится без остатка на (bk-a).