Свойство 3

Разность не зависит от порядка, в котором расположены ее аргументы

Доказательство вытекает из свойства 1.

Если степень многочлена f (x) равна n, то разность 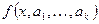порядка k есть многочлен степени n-k при n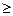k и 0 при n<k.

Доказательство проведём индукцией по k. При k=1 имеем . Числителем дроби является многочлен 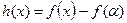, причём . Следовательно, по теореме Безу многочлен делится без остатка на двучлен 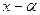. Тем самым основание индукции доказано. Пусть утверждение верно для разностей порядка k-1. Покажем его справедливость для разностей порядка k. По определению разности порядка k имеем 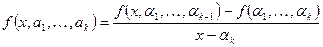. По предположению индукции числитель этой дроби 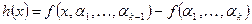многочлен степени n-k+1. Кроме того 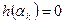(свойство 2) и по теореме Безу многочлен делится без остатка на двучлен . Свойство доказано.