Объединение
А È В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности
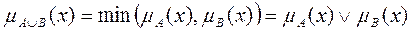 .
.
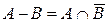 с функцией принадлежности
с функцией принадлежности
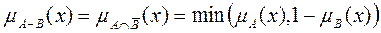 .
.
Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения 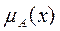 , а на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (рис. 4.1).
, а на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (рис. 4.1).

Рис. 4.1. Графическая интерпретация логических операций
Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм.
Треугольной нормой (Т-нормой) называется двуместная действительная функция Т: [0,1]´[0,1]®[0,1], удовлетворяющая следующим условиям:
1) Т (0,0)=0; Т ( ,1)=
,1)=  ; Т (1,
; Т (1,  )=
)= – ограниченность;
– ограниченность;
2) Т ( ,
,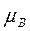 ) £ Т (
) £ Т (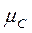 ,
,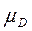 ), если
), если  £
£ 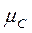 ,
, 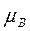 £
£ 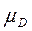 – монотонность;
– монотонность;
3) Т ( ,
,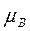 ) = Т (
) = Т (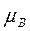 ,
, ) – коммутативность;
) – коммутативность;
|
|
|
4) Т ( , Т (
, Т (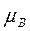 ,
,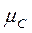 )) £ Т (Т (
)) £ Т (Т ( ,
,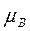 ),
), 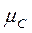 ) – ассоциативность.
) – ассоциативность.
Простым случаем треугольных норм являются:
– min ( ,
,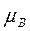 ),
),
– произведение  ×
×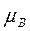 ,
,
– max (0,  +
+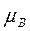 -1).
-1).
Треугольной конормой (Т-конормой или S-нормой) называется двуместная действительная функция S: [0,1]´[0,1]®[0,1], со свойствами:
1) S (1, 1)=1; S ( , 0)=
, 0)= ; S (0,
; S (0,  )=
)= – ограниченность;
– ограниченность;
2) S ( ,
,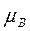 )³ S (
)³ S (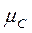 ,
,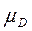 ), если
), если  ³
³ 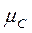 ,
, 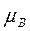 ³
³ 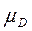 – монотонность;
– монотонность;
3) S ( ,
,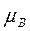 ) = S (
) = S (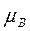 ,
, ) – коммутативность;
) – коммутативность;
4) S ( , S (
, S (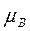 ,
, 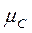 )) £ S (S (
)) £ S (S ( ,
, 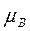 ),
), 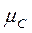 ) – ассоциативность.
) – ассоциативность.
Примеры Т-конорм:
– max ( ,
,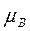 ),
),
–  +
+ 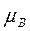 –
–  ×
×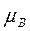 ,
,
– min (1,  +
+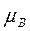 ).
).
Алгебраические операции
Теперь представим алгебраические операции с нечеткими множествами.
Алгебраическое произведение А и В обозначается А×В и определяется так:
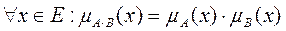 .
.
Алгебраическая сумма этих множеств обозначается А 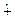 В и определяется так:
В и определяется так:
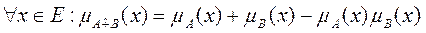 .
.
На основе операции алгебраического произведения определяется операция возведения в степень a нечеткого множества А, где a – положительное число. Нечеткое множество Аa определяется функцией принадлежности 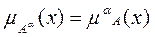 . Частными случаями возведения в степень являются:
. Частными случаями возведения в степень являются:
– CON(А)= А2 – операция концентрирования (уплотнения),
– DIL(А)= А0,5 – операция растяжения,
которые используются при работе с лингвистическими неопределенностями.
Декартово (прямое) произведение нечетких множеств. Пусть А1, А2,…, Аn – нечеткие подмножества универсальных множеств Е1, Е2,…, Еn соответственно. Декартово или прямое произведение А = А1 ´ А2 ´…´ Аn является нечетким подмножеством множества Е = Е1 ´ Е2 ´…´ Еn с функцией принадлежности
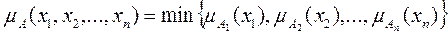 .
.
11 ЛЕКЦИЯ 2 ЧАСА
 2014-02-02
2014-02-02 607
607







