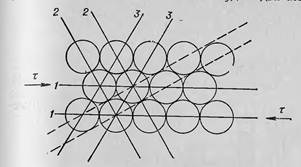
Пластическая деформация в кристаллах может осуществляться скольжением и двойникованием. Скольжение (смещение) отдельных частей кристалла относительно друг друга происходит под действием касательных напряжений, когда эти напряжения в плоскости и в направлении скольжения достигают определенной критической величины (τк). Скольжение в кристаллической решетке протекает по плоскостям и направлениям с наиболее плотной упаковкой атомов, где величина сопротивления сдвигу наименьшая. Это объясняется тем, что расстояние между соседними атомными плоскостями наибольшее, т. е. связь между ними наименьшая (на рисунке плоскости скольжения 1 – 1, 2 – 2, 3 – 3, в отличие от плоскостей скольжения, показанных штриховыми линиями). Плоскости скольжения и направления скольжения, лежащие в этих плоскостях, образуют систему скольжения. В металлах могут действовать одна или одновременно несколько систем скольжения.
 |  |
Под действием внешней силы первой «заработает» та группа параллельных плотноупакованных плоскостей, которые составляют с осью растяжения угол 45 градусов. На площадках расположенных под этим углом к оси растяжения, касательные напряжения максимальны. Деформирование поликристаллических металлов, состоящих из множества зерен – монокристаллов, сопровождается сдвигом одних слоев металла в пределах каждого зерна относительно соседних по плоскостям скольжения. В результате каждое зерно вытягивается в осевом направлении и сжимается в двух других. (Чем больше в металле возможных плоскостей и направлений скольжения, тем выше его способность к пластической деформации. Металлы, имеющие кубическую кристаллическую решетку, обладают высокой пластичностью, так как скольжение в них происходит во многих направлениях. Металлы с гексагональной плотноупакованной структурой менее пластичны и поэтому труднее, чем металлы с кубической структурой, поддаются прокатке, штамповке и другим способам деформации).
Многочисленные эксперименты показывают, что плотность металлов при их пластической деформации практически не изменяется.
Процесс скольжения не следует, представлять как одновременное передвижение одной части кристалла относительно другой. Такой синхронный, сдвиг потребовал бы напряжений, в сотни или даже тысячи раз превышающие те, при которых в действительности протекает процесс деформации. (Касательное напряжение, необходимое для начала скольжения – одного порядка с модулем сдвига. Например для чистого железа G = 8·104 МПа, а τупр ≈ 10 МПа. Расчеты Я.И.Френкеля).
Скольжение осуществляется в результате перемещения в кристалле дислокаций.
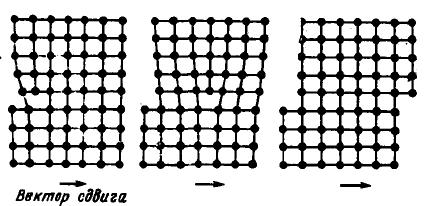  |
Все атомы, участвующие в движении дислокации смещаются на расстояния, порядка межатомного. Если мы взглянем на кристалл (рисунок), то дислокация спроектируется в прямую линию которая будет стремится занять симметричное положение между двумя соседними плоскостями (позиция 4). Эта линия должна будет перейти в соседнюю аналогичную позицию, преодолев барьер, обозначенный пунктиром. Вначале в новое положение переходит лишь небольшая часть дислокации – позиция 5, а затем вся остальная.
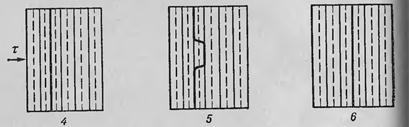
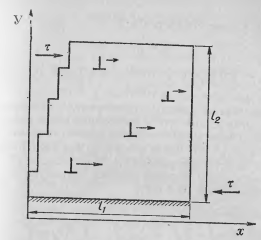
Сколько дислокаций необходимо для обеспечения сдвиговой деформации заданной величины. Предположим, что касательное напряжение τ стремится вызвать сдвиг γ вправо части кристалла размерами l1 и l2. Когда дислокации пробегут путь l1 от левой до правой грани кристалла, каждая из них даст на поверхности ступеньку величиной b. Пока ступенька есть только на левой грани кристалла, значит изменение его размера в направлении оси x, связанное с одной дислокацией, меньше b. Это изменение размера δ, составляет такую же долю от b, какую пробег дислокации x от l1: 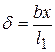 . При x= l1, получим δ=b. Полное изменение Δ, размера кристалла в направлении оси x будет равно сумме смещений δ, связанных с каждой дислокацией:
. При x= l1, получим δ=b. Полное изменение Δ, размера кристалла в направлении оси x будет равно сумме смещений δ, связанных с каждой дислокацией:
Δ = δ1+ δ2+…+ δn = (bnx)/ l1, где n – число дислокаций, x – усредненная по всему кристаллу длина пробега дислокаций. Относительная деформация сдвига в плоскости xy равна изменению размера вдоль оси x, деленному на исходный размер вдоль оси y:
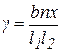 .
.
Но 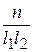 – плотность дислокаций ρ, поэтому приняв, что средний пробег дислокаций равен среднему расстоянию между ними
– плотность дислокаций ρ, поэтому приняв, что средний пробег дислокаций равен среднему расстоянию между ними 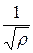 , получим
, получим 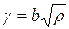 . В металлических кристаллах b равно (2 – 3)·10-8 см, для получения деформаций порядка процентов необходимо ~ 1013 дислокаций на 1 см2.
. В металлических кристаллах b равно (2 – 3)·10-8 см, для получения деформаций порядка процентов необходимо ~ 1013 дислокаций на 1 см2.
Такая плотность дислокаций близка к предельной, так как среднее расстояние между ними порядка десятка межатомных расстояний. В кусочке сильно деформированного металла размером с булавочную головку суммарная длина дислокационных линий превышает расстояние от Земли до Луны.
  |
Типичные значения плотности дислокаций в металле после затвердевания 106 – 108 см2.
 2014-02-02
2014-02-02 1725
1725








