Проекции ускорения на естественные оси. Касательное и нормальное ускорения

Реализация решения

• Реальная ценность решения становится очевидной только после его осуществления.

• Уровень эффективности осуществления решения повысится, если оно будет принято теми, кого оно затрагивает.

Пусть точка движется по криволинейной траектории и пусть в момент времени t она занимает положение М, а в момент t+Δt положение М' на траектории (рис.12.1).

Рис.12.1.

Длину элементарной дуг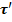и и ,построенных в точка М и М'. Чтобы найти вектор 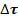, перенесем вектор и 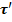, т.е.:

=1. Угол при вершине М равен углу смежности (углу между касательными в точках М и М'), который обозначим через Δφ в радианах. Отсюда следует, что , поэтому

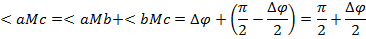
Следовательно, в пределе при 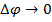угол становится прямым, и следовательно, направление вектора 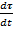совпадает с положительным направлением главной нормали, т.е. с направлением орта n.

Найдем модуль этого вектора. Из равнобедренного треугольника аМb имеем:

Но Ма=1 и аb=Мс=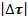, следовательно 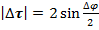, отсюда

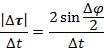
Переходя к пределу, получим:

Или

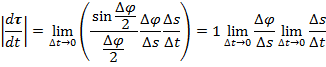
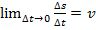, следовательно,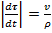

Итак мы установили, что вектор 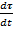направлен по главной нормали к центру кривизны и по модулю равен . Следовательно, .

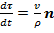Подставляя это значение производной 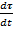в полученное выше выражение ускорения 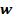,получим:

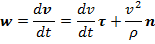
Эта формула дает разложение ускорения 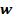по естественным осям. Вектор 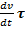направлен по той же прямой, что и вектор , т.е. по касательной (рис.12.2) и по модулю равен – этот вектор называется касательным или тангенциальным ускорением и обозначается через 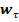и, следовательно, равен:

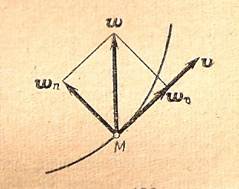Рис.12.2.

Вектор 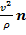направлен по главной нормали и по модулю равен 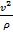- этот вектор называется нормальным ускорением и обозначается через 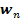(рис.12.2), следовательно:

Так как оба вектора лежат в соприкасающейся плоскости, то, следовательно, ускорение 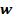также лежит в соприкасающейся плоскости.

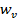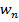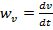Если обозначим проекцию ускорения на касательную (на направление скорости), через , а проекцию на главную нормаль через , то и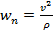

Т.е. проекция ускорения на направление скорости равна производной от модуля скорости по времени, а проекция ускорения на главную нормаль равна квадрату скорости, разделенному на радиус кривизны траектории в той ее точке, где в данный момент находится движущаяся точка. Так как ускорение лежит в соприкасающейся плоскости, то его проекция на бинормаль равна нулю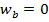

Для модуля ускорения 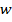получаем формулу:

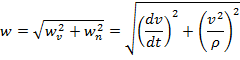
Если модуль скорости с течением времени возрастает, то точка движется ускоренно, то производная положительна. В этом случае касательное ускорение 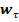направлено по касательной в сторону движения точки, т.е. в ту же сторону, что и скорость .

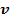В случае замедленного движения производная отрицательна, и ускорение 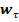направлено по касательной в сторону противоположную скорости. Что касается нормального ускорения 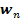, то оно направлено всегда по главной нормали в сторону вогнутости траектории (к центру кривизны), так как величина 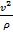всегда положительна и, следовательно, направление вектора 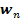совпадает с направлением орта .

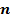Найдем проекцию 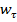ускорения на касательную:

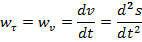
Проекция ускорения на касательную, положительное направление которой совпадает с положительным направлением отсчета дуговой координаты движущейся точки, равна второй производной от этой дуговой координаты по времени.

Производная 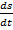представляет собой алгебраическое значение скорости, т.е. проекцию вектора 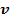на касательную при вышеуказанном положении орта касательной .

Так как проекция ускорения на главную нормаль выражается через квадрат скорости, то независимо от знака производной 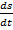имеем:

Тогда формулу модуля ускорения можно представить в виде:

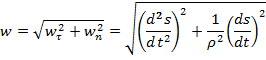
Рассмотрим некоторые частные случаи движения точки.

1. Прямолинейное движение. В этом случае 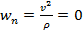, так как для прямой линии 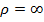. Следовательно, направление ускорения 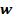или совпадает с направлением движения (направлением скорости 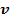), или противоположно этому направлению в зависимости от знака производной . По модулю ускорение 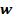в этом случае равно абсолютной величине производной .

2. Равномерное криволинейное движение. Так как при равномерном движении точки модуль скорости остается постоянным, т.е. 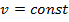, то в этом случае

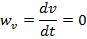
Ускорение 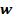направлено по главной нормали в сторону вогнутости траектории и по модулю равно .

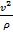3. Равномерное прямолинейное движение. В этом случае 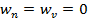, т.е. .

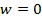Таким образом, касательное ускорение возникает в тех случаях, когда изменяется модуль скорости, т.е. при неравномерном движении очки, а нормальное ускорение – в том случае, когда изменяется направление скорости, т.е. при криволинейном движении точки.

Т.е. касательное ускорение характеризует изменение скорости по модулю, а нормальное ускорение характеризует изменение скорости по направлению.

При неравномерном движении касательное ускорение обращается в нуль в те моменты, когда производная 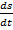достигает максимума или минимума, так как в эти моменты вторая производная .

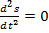Нормальное ускорение в криволинейном движении равно нулю на тех точках траектории, где 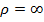, т.е. в точках перегиба траектории. Кроме того нормальное ускорение становится равным нулю в те моменты, когда изменяется на противоположное направление движения точки по заданной траектории, так как в эти моменты производная 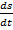, меняя знак становится равной нулю.