Определение. Выборочной средней 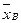 называется среднее арифметическое значений признака выборочной совокупности.
называется среднее арифметическое значений признака выборочной совокупности.
Если все значения 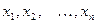 признака выборки объёма n различны, то
признака выборки объёма n различны, то
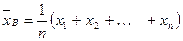 . (4)
. (4)
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты 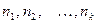 , причём
, причём 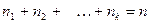 , то
, то
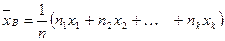 (5)
(5)
или
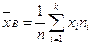 .
.
Пример. Выборочным путём были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28, 27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найти выборочную среднюю 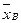 .
.
По формуле (5):
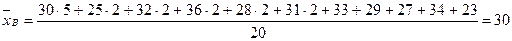 .
.
Определение. Выборочной дисперсией 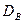 называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней 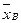 .
.
Если все значения 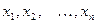 признака выборки объёма n различны, то
признака выборки объёма n различны, то
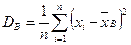 . (9)
. (9)
Если же значения  признака имеют соответственно частоты
признака имеют соответственно частоты 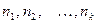 , причём
, причём 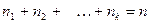 , то
, то
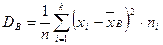 . (10)
. (10)
Пример. Выборочная совокупность задана таблицей распределения:
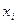 | ||||
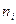 |
Найти выборочную дисперсию.
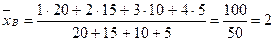 ;
;
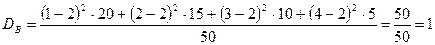 .
.
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии: 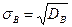 .
.
Пример. 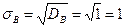
Модой называется значение признака, наиболее часто встречающееся в совокупности, в ряде распределения.
Медианой в статистике называется значение признака, которое делит численность упорядоченного ряда распределения на две равные части.
Размахом варьирования признака называется R=Xmax-Xmin, т.е. разность между максимальным и минимальным значениями.
 2014-02-02
2014-02-02 2395
2395







