Экстремальные графы

Задача Рамсея

Широко известна следующая головоломка.

Доказать, что среди любых шести человек найдутся либо трое попарно знакомых, либо трое попарно незнакомых. Указанную ситуацию можно описать графом G с шестью вершинами, представляющими людей; смежность двух вершин соответствует знакомству. Требуется показать, что в G найдутся либо три попарно смежные, либо три попарно несмежные вершины.

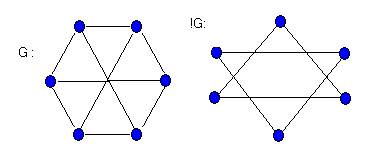
Дополнение G графа G имеет в качестве множества вершин множество V(G), две вершины в G смежны тогда и только тогда, когда они не смежны в G. На рис. в графе G нет треугольников, а в графе G их ровно два. Самодополнительный граф - это граф, изоморфный своему дополнению. Примеры таких графов приведены на рисунке.

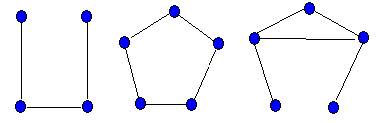
В полном графе Кр каждая пара его р вершин смежна. Таким образом, граф Kp имеет (P2) ребер и является регулярным степени p-1. Граф K₃—треугольник. Графы!Кр— вполне несвязные (или регулярные степени 0).

В этих терминах головоломку можно сформулировать так:

Теорема. Если G-граф с шестью вершинами, то либо G, либо!G содержит, треугольник.

Доказательство. Пусть v — произвольная вершина графа G, имеющего шесть вершин. Так как вершина v с любой из остальных пяти вершин смежна или в G, или в G, то, не теряя общности, можно предположить, что вершины u1,u2,u3 смежны с v в G. Если какие-либо две из вершин u1,u2,u3, смежны в G, то вместе с v они образуют треугольник. Если никакие две из них не смежны в G, то в графе G вершины u1,u2,u3 образуют треугольник.

Обобщая теорему, естественно поставить вопрос: каково наименьшее целое число r(m, n), для которого каждый граф с r(m, n) вершинами содержит Кm или Kn

Числа r (m, n) называются числами Рамсея. Ясно, что r (m, n) = r(n, m). Задача, связанная с нахождением чисел Рамсея, остается нерешенной, хотя известна простая верхняя оценка, полученная Эрдёшем и Секерешем:

r(m,n)£(m+n-2, m-1)

Постановка этой задачи вытекает из теоремы Рамсея. Бесконечный граф имеет бесконечное множество вершин и не содержит кратных ребер и петель. Рамсей доказал (на языке теории множеств), что каждый бесконечный граф содержит #0 попарно смежных вершин или #0 попарно несмежных вершин.

Все известные числа Рамсея приведены в табл.

2 3 4 5 6 7

2 2 3 4 5 6 7

3 3 6 9 14 18 23

4 4 9 18

Среди первых результатов в одном из направлений теории графов - теории экстремальных графов - можно отметить следующую известную теорему Турана [1]. Как обычно, пусть [r] - наибольшее целое число, не превышающее действительного числа r, а {r} = есть наименьшее целое число, не меньшее r.

Теорема: Наибольшее число ребер у графов, имеющих р вершин и не содержащих треугольников, равно [р2/4].

Доказательство: Утверждение очевидно для малых значений р. Доказательство по индукции можно дать отдельно для нечетных и для четных р; здесь будет рассмотрен только случай четных значений р. Предположим, что утверждение справедливо для всех четных значений р<=2п. Докажем его для р=2n+2. Итак, пусть G — граф с р=2n+2 вершинами, не содержащий треугольников. Поскольку граф G не является вполне несвязным, то в нем существуют две смежные вершины u и v. В подграфе G' = G — {и, v} имеется 2n вершин и нет треугольников, так что по предположению индукции в графе G' самое большее [4n2/4] = n2 ребер. Сколько еще ребер может быть в графе G? В графе G нет такой вершины w, что вершины u и v одновременно смежны с w, т. е. вершины и, v и w образуют в графе G треугольник. Таким образом, если вершина u смежна с k вершинами графа G', то вершина v может быть смежна самое большее с 2n—k вершинами. Поэтому в графе G не больше чем

n2+k+(2n—k)+l = n2+2n+1=p*p/4=[p²/4] ребер.

Для завершения доказательства осталось установить, что для каждого четного р существует (р, Р²/4)-граф, не содержащий треугольников. Такой граф можно образовать следующим образом: возьмем два множества V1 и V2, каждое из которых имеет р/2 вершин, и соединим каждую вершину из V1 с каждой вершиной из V2.

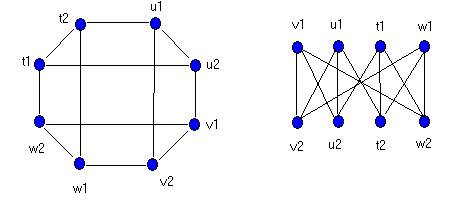
Двудольный граф (или биграф) G - это граф, множество вершин V которого можно разбить на два подмножества V1 и V2 таким образом, что каждое ребро графа G соединяет вершины из разных множеств (будем говорить, что ребра графа G соединяют множества V1 и V2)- Например, граф, представленный на рис. слева, можно нарисовать так, как показано на рисунке справа, чтобы подчеркнуть, что этот граф - двудольный.

Если граф G содержит все ребра, соединяющие множества V1 и V2, то этот граф называется полным двудольным. Если при этом в множестве V1 имеется m вершин а в V2 имеется n вершин, то будем писать G = Km,n.= K(m, n). Звездой называется полный двудольный граф К₁,n. Понятно, что в графе Кm,n имеется mn ребер. Поэтому, если р четно, то граф К (р/2, р/2) содержит р2/4 ребер; если р нечетно, то граф К ([р/2], {р/2}) содержит [р/2] {р/2} = [p2/4] ребер. В каждом из таких графов нет треугольников, что следует из теоремы Кёнига

Теорема: Граф является двудольным тогда и только тогда, когда все его простые циклы четны.

Доказательство. Если G — двудольный граф, то множество его вершин V можно разбить на два подмножества V1 и V2 таким образом, что любое ребро этого графа соединяет некоторую вершину из множества V1 с некоторой вершиной из V2. Поэтому каждый простой цикл v1v2... vnv1 графа G содержит вершины из V1, скажем, с нечетными номерами и вершины из V2 с четными, так что длина n этого цикла является четным числом.

Чтобы доказать обратное, предположим, не теряя общности, что G — связный граф (поскольку каждую компоненту графа G можно рассматривать отдельно). Возьмем произвольную вершину vj Î V и обозначим через V1 множество, состоящее из v1 и всех вершин, находящихся в графе G на четном расстоянии от v1; пусть V2= V-V1. Так как все простые циклы графа G четны, то каждое его ребро соединяет множества V1 и V2. В самом деле, если существует ребро uv, соединяющее две вершины из множества V2, то объединение геодезических, идущих из вершины v1 к вершине u, а также из вершины v1 к вершине u, вместе с ребром uv образует цикл нечетной длины; мы пришли к противоречию.

Теорема является первым примером решения одной из задач «теории экстремальных графов»: для данного графа Н найти ех(р, Н) — наибольшее число ребер, которое может быть в графе, имеющем р вершин и не содержащем запрещенный подграф H. Таким образом, в теореме утверждается, что ех (р, К3) = [p*p/4]. Приведем некоторые другие подобные результаты (Эрдёш [3]):

ex(p,Cp) = 1 + (p(p+1))/2

ex(p,K4-x) = [p*p/4]

ex(p,K1,3 + x) = [p*p/4]

Известно также, что каждый (2п,n*n+1)-граф содержит n треугольников, каждый (р, Зр-5)-граф содержит два простых цикла, не имеющих общих ребер (для р>= 6), и каждый (Зn, 3n₂ + 1)-граф содержит n₂ простых циклов длины 4.