 .
.
Пример. Выполнить суммирование двоичных чисел 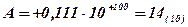 и
и 
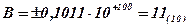 с представлением мантиссы шестью разрядами.
с представлением мантиссы шестью разрядами.
Так как РА=РВ, то выравнивание порядков не требуется. Для случая В>0 нахождение суммы S проведём используя прямой код.
| порядок | знак | мантисса | |
| +А | |||
| В | |||
Так как возникло переполнение поля разрядной сетки, отведённого под мантиссу, проведём нормализацию результата вправо на один разряд, соответственно увеличив значение порядка на единицу, т. е.
 0 0
|
В итоге получим результат 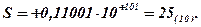
Для случая В<0 нахождение суммы S проведём используя дополнительный код (мантиссы суммируются в дополнительном коде).
| порядок | знак | мантисса в доп. коде | |
| +А | |||
| В | |||
| S |
Так как возникло совпадение цифр в знаковом разряде и старшем разряде мантиссы, то проведём нормализацию результата влево на два разряда, соответственно уменьшив значение порядка на два, т. е.
| S | 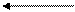 0 0
| ||
| S |
В итоге получим результат 
|
|
|
Задание 35. Выполнить суммирование двоичных чисел 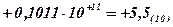 и
и 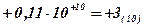 .
.
Задание 36. Выполнить суммирование двоичных чисел +1101,11 и -1000,01 в форме с ПЗ.
Задание 37. Выполнить суммирование двоичных чисел 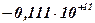 и
и 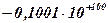 .
.
1.2.3. Сложение и вычитание чисел в двоично-десятичных кодах (Д-кодах).
| … | …. |
Соответствие десятичных цифр их двоично-десятичным кодам дано таблицей.
Такое кодирование применяется при записи десятичных чисел в зонном и упакованном формате.
Сложение чисел в Д-кодах сводится к суммированию тетрад, соответствующих их разрядам, по правилам двоичной арифметики и коррекции тетрад суммы. Для тетрад суммы, значение которых превышают 1001, необходимо организовать перенос в следующую тетраду и выполнить коррекцию. Коррекция представляет собой вычитание 1010, что соответствует сложению тетрады с 0110 без переноса (т. к. 0110 есть дополнительный код числа 1010).
Пример. Определить сумму чисел А=753(10) и В=439(10) в двоично-десятичном коде.
Представим числа А и В в Д-коде и выполним суммирование:
| +А | = | |||
| В | = | |||
| S’ | = | |||
| выполним коррекцию | +0110 | +0110 | ||
| S | = 1 |
,что соответствует 1192(10).
Вычисление чисел в Д-кодах выполняется так же, как и вычисление двоичных чисел, т. е. вычисляемое представляется в дополнительном коде, а операция вычисления сводится к сложению. Дополнительный код числа, представленного Д-кодом, формируется дополнением каждой тетрады до 1001 и добавлением к младшей тетраде единицы.
Пример. Определить разность чисел А=753(10) и В=439(10) в двоично-десятичном коде.
Представим число В в дополнительном коде
| -1001 | -1001 | -1001 | дополнение каждой тетрады до 1001 | |
| добавление к младшей тетраде единицы | ||||
| +1 | ||||
| Вдоп= |
Теперь выполним операцию S=А-В=А+Вдоп.
|
|
|
| +А | |||
| Вдоп | |||
| S’ | |||
| коррекция | +0110 | +0110 | |
| S |
, что соответствует 314(10).
Задание 38. Выполнить сложение чисел 280(10) и 157(10) в Д-коде.
Задание 39. Определить разность чисел 1092(10) и 956(10) в Д-коде.
1.2.4. Умножение и деление двоичных чисел.
Ограничимся рассмотрением выполнения операций умножения и деления над двоичными числами в прямом коде с учётом их знаков. Эти операции выполняются с многократным применением операций сложения и сдвига и могут быть реализованы схемой показанной на рисунке.

Операция умножения чисел А и В выполняется в несколько тактов. Множимое А записывается в Рег.1, а множитель В в Рег.3. Рег.2 предварительно устанавливается в 0. На каждом такте анализируется содержимое старшего (левого) разряда Рег.3. Если в нём находится 1-ца, то производится общий сдвиг влево содержимого Рег.3 и Рег.2 (с переносом между ними) и суммирование содержимого регистров Рег.1 и Рег.2 с занесением результата в Рег.2. Если в старшем разряде Рег.3 находится 0, то производится лишь сдвиг влево содержимого Рег.3 и Рег.2. Число тактов равно числу разрядов множителя В. В результате произведение будет располагаться в Рег.3 и Рег.2.
Код знака результата операции умножения получаем суммированием по mod2 кодов знаков сомножителей (логическая функция сложения по mod2 показана далее).
Пример. Выполнить умножение чисел А=11(10)=1011(2) и В=13(10)=1101(2).
| х1011 |
Для наглядности последующих действий предварительно умножим числа «в столбиках».
Теперь рассмотрим выполнение операции умножения схемой, представленной на рис. 1.
Операция проводится в 4 такта (число В четырёхразрядное).
Начальное содержимое регистров:
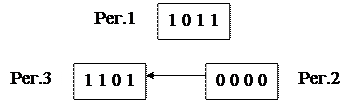 |
Такт 1. Так как в старшем разряде Рег.3 находится 1-ца, то производится сдвиг содержимого Рег.3 и Рег.2 и суммирование содержимого Рег.1 и Рег.2 с записью результата в Рег.2.
|
|
|
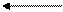
|
Такт 2. В старшем разряде Рег.3 опять 1-ца, следовательно, в результате сдвига и суммирования получим:
 | ||||||
|
| |||||
Такт 3. В старшем разряде Рег.3 находится 0, поэтому производится только сдвиг.
 | ||||||
|
| |||||
Такт 4. В старшем разряде Рег.3 опять 1-ца. Выполняются сдвиг и суммирование.
 | ||||||
|
| |||||
Проверим правильность выполнения умножения.
10001111(2)=143(10), т. е. 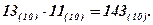
Задание 40. Выполнить операцию умножения чисел 14(10) и -9(10) реализуя алгоритм работы схемы рис. 1.
Задание 41. Выполнить операцию умножения чисел -19(10) и -7(10), реализуя алгоритм работы схемы рис. 1.
Операция деления чисел А и В выполняется схемой рис. 1 также за несколько тактов. Делимое А располагается одновременно в Рег.3 и Рег.2, а делитель В в Рег.1. На каждом такте сравнивается содержимое Рег.3 и Рег.1. Если число в Рег.3 больше числа в Рег.1, то производится:
- вычитание из содержимого Рег.3 содержимого Рег.1 с записью результата в Рег.3;
- общий сдвиг влево содержимого Рег.3 и Рег.2 (с переносом между ними);
- запись 1-цы в младший разряд Рег.2.
Если число в Рег.3 меньше числа в Рег.1, то производится лишь сдвиг влево содержимого Рег.3 и Рег.2. Итоговый результат операции деления будет располагаться в Рег.2.
Код знака результата операции деления получается аналогично коду знака результата операции умножения.
Пример. Выполнить деление числа 143(10)=10001111(2) на число 11(10)=1011(2).
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||
Для наглядности последующих действий предварительно разделим числа «в столбик».
|
|
|
Теперь рассмотрим выполнение операции деления схемой, представленной на рис.1. Начальное содержимое регистров:
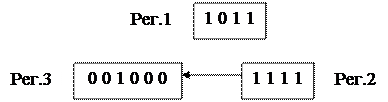 |
Такт 1. Так как число в Рег.3 меньше числа в Рег.1 то производится общий сдвиг влево содержимого Рег.3 и Рег.2. Получим
 |
Такт 2. Теперь число в Рег.3 больше числа в Рег.1, поэтому производится вычитание из содержимого Рег.3 содержимого Рег.1 с записью результата в Рег.3.
 |
а затем выполняется общий сдвиг всего содержимого Рег.3 и Рег.2 и запись 1-цы в младший разряд Рег.2 Получим
 |
Такт 3. Так как сейчас число в Рег.3 больше числа в Рег.1, то действия предыдущего такта повторяются. После вычитания получим
 |
а после сдвига влево в Рег.3 и Рег.2 и записи 1-цы в младший разряд Рег.2 будем иметь
 |
Такт 4. В этом случае число в Рег.3 стало меньше числа в Рег.1, поэтому производится только общий сдвиг влево Рег.3 и Рег.2
 |
 Такт 5. Теперь опять число в Рег.3 больше числа в Рег.1. Поэтому выполняется вычитание
Такт 5. Теперь опять число в Рег.3 больше числа в Рег.1. Поэтому выполняется вычитание
сдвиг и запись 1-цы в младший разряд Рег.2
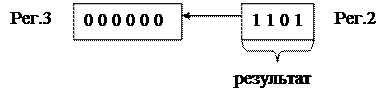 |
Проверим правильность выполнения деления:
1101(2)=13(10), т. е. 143(10):11(10)=13(10).
Замечание. Чтобы реализовать операцию вычитания в сумматоре (рис.1) нужно заменить её операцией сложения с числом в дополнительном коде, т. е. к содержимому Рег.3 прибавлять содержимое Рег.1 взятое в дополнительном коде. В рассмотренном примере вычиталось число 1011, следовательно нужно прибавлять число 0101. (Проверить самостоятельно).
Задание 42. Выполнить операцию деления чисел 126(10) и 14(10), реализуя алгоритм работы схемы рис.1.
Задание 43. Выполнить операцию деления чисел 123(10) и -7(10), реализуя алгоритм работы схемы рис.1.
Замечание. При выполнении операции умножения и деления чисел в форме с ПЗ необходимо выполнить:
|
|
|
- умножение или деление мантисс исходных чисел (по алгоритмам рассмотренным выше);
- определение порядка результата (получается соответственно сложением или вычитанием порядков исходных чисел с учётом их знаков);
- нормализацию результата с соответствующей коррекцией порядка.
1.3. Логические основы вычислительной техники.
Комбинационные схемы и конечные автоматы.
Устройство преобразовывающее информацию
 |
Входной и выходной сигналы.
В цифровой вычислительной машине (ЦВМ) время дискретно, т. е. переход от 0 в 1 за момент. Интервал между моментами – такт.
 |
Преобразующее устройство Р:
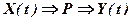 , где X(t)={x1, x2 … xn} – множество входных дискретных тактиров-х сигналов, Y(t)={y1, y2 … ym} – множество выходных сигналов, Р – функция или функционал преобразования.
, где X(t)={x1, x2 … xn} – множество входных дискретных тактиров-х сигналов, Y(t)={y1, y2 … ym} – множество выходных сигналов, Р – функция или функционал преобразования.
Если элементарный сигнал может быть представлен с различными состояниями:
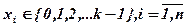

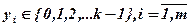 то можно ввести понятие k-значной логики.
то можно ввести понятие k-значной логики.
k-значной логикой называют математический аппарат, позволяющий описать функционирование Р-преобразователей. k-значная логика может приведена быть к 2-ой логике, т. к. k-значную переменную можно заменить на log2k двоичных переменных.
Поэтому дальше 2-ая (Булева) логика.
Устройство реализующее Р называется в ЦВМ автоматом.
2 вида дискретных автоматов:
1) Если совокупность выходных сигналов (выходного слова) Y(t) зависит от X(t) и не зависит от внутреннего состояния автомата, то это комбинационная схема. Y(t)=P[X(t)].
Структурная схема: 
ЭП комбинационный автомат не содержит.
Закон функционирования комбинационного автомата определяется заданием соответствия между входным и выходным словами.
Можно задать: таблицей
аналитически (булевыми функциями)
2) Если Y(t)=P[X(t), S(t-1)], то автомат с памятью (конечный).
r+1 внутренних состояний S(t)={S0, S1, … Sr}. При подаче X(t) в t-ом такте автомат переходит их S(t-1) в S(t). Структурная схема
 |
КС – комбинационная схема.
Одновременность сигналов на комбинационной схеме обеспечивается синхронизацией (тактируемостью сигнала).
Элементы теории конечных автоматов в главе 3.
1.3.1. Переключательные (булевы, логические) функции.
I. Основные понятия и определения.
| x1 | x2 | … | xn | f(x1…xn) |
| … | … | … … … … | … | 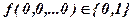 …
…
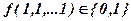
|
Булевой функцией называется f(x1, x2, … xn), аргументы которой 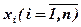 и сами функции принимают значение из множества Е2={0,1}. Они могут быть заданы таблицей. Полная таблица функции от n переменных имеет 2n строк и n+1 столбцов. Упорядоченная таблица называется таблицей истинности. Другая форма – булевы выражения.
и сами функции принимают значение из множества Е2={0,1}. Они могут быть заданы таблицей. Полная таблица функции от n переменных имеет 2n строк и n+1 столбцов. Упорядоченная таблица называется таблицей истинности. Другая форма – булевы выражения.
Теорема: число различных переключательных функций n-аргументов равно 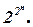
Определение: Две переключательных функции называются равными, если на всех наборах аргументов они принимают одинаковые значения.
Определение: Переключательная функция f называется существенно зависимой от xi, если выполняется неравенство: 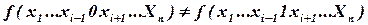 . Не все переключательные f существенно зависимы.
. Не все переключательные f существенно зависимы.
Определение: Переключательная функция f независящая ни от одного аргумента и равная 0 (1) на всех наборах называется нулевой (единичной).
II. Элементарные логические функции.
Называются функции 1 или 2-х аргументов.
Логическая функция 1-ой переменной:
| x | ||
| f1(x) f2(x) f3(x) f4(x) |
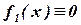 - нулевая функция;
- нулевая функция;
 - функция повторения аргумента
- функция повторения аргумента
 - функция инверсии аргумента
- функция инверсии аргумента
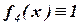 - единичная функция
- единичная функция
Логические функции 2-х переменных:
| функции | аргументы х1 0011 х2 0101 | обозначение функции | название функции и комментарии |
| f0(x1,x2) | 0 0 0 0 | Нулевая | |
| f1(x1,x2) | 0 0 0 1 | x1 Ù x2 | Конъюнкция |
| f2(x1,x2) | 0 0 1 0 | 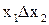
| запрет по х 2 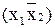
|
| f3(x1,x2) | 0 0 1 1 | х1 | повторение х1 |
| f4(x1,x2) | 0 1 0 0 | 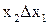
| запрет по х 1 |
| f5(x1,x2) | 0 1 0 1 | х2 | повторение х2 |
| f6(x1,x2) | 0 1 1 0 | 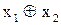
| сумма по mod2 |
| f7(x1,x2) | 0 1 1 1 | 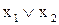
| Дизъюнкция |
| f8(x1,x2) | 1 0 0 0 | 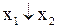
| стрелка Пирса 
|
| f9(x1,x2) | 1 0 0 1 | 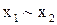
| эквивалентность (равнозначность) |
| f10(x1,x2) | 1 0 1 0 | 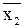
| отрицание х2 |
| f11(x1,x2) | 1 0 1 1 | 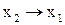
| импликация от х 2 к х 1 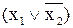
|
| f12(x1,x2) | 1 1 0 0 | 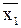
| отрицание х1 |
| f13(x1,x2) | 1 1 0 1 | 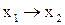
| импликация от х 1 к х 2 (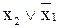 ) )
|
| f14(x1,x2) | 1 1 1 0 | x1\x2 | штрих Шеффера 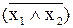
|
| f15(x1,x2) | 1 1 1 1 | Единичная |
III. Системы элементарных логических функций.
Определение: Набор элементарных логических функций, используемый для записи любых логических выражений называется системой логических функций (СЛФ).
Определение: Набор элементарных логических функций достаточный для записи любых логических выражений называется функционально полной СЛФ (ФП СЛФ).
Определение: Если исключение любой элементарной логической функции из ФП СЛФ приводит к функциональной неполноте, то исходная ФП СЛФ называется безызбыточной. Иначе ФП СЛФ называется избыточной.
Теорема о функциональной полноте СЛФ (Постников, Яблонский).
СЛФ называется функционально полной в том и только том случае, если она включает хотя бы одну функцию, не принадлежащую к 5 важнейшим замкнутым классам:
1) – класс функций сохраняющих 0,
2) – класс функций сохраняющих 1,
3) – класс самодвойственных функций,
4) – класс монотонных функций,
5) – класс линейных функций.
Рассмотрим классы:
1) f (0, 0, … 0) = 0
2) f (1, 1, … 1) = 1 т. е. если подставить 0-е значение аргументов, то функция =0 или 1
3) 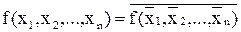
4) Пусть х1i=1, a x1j=0. Тогда x1i>x1j. Функция f(x1, x2, … xn) является монолитной, если для всех случаев, когда 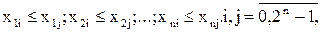 во всех наборах выполняется неравенство
во всех наборах выполняется неравенство 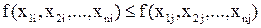
| х1 | 0(х10) | 1(х11) | 1(х12) |
| х2 | 0(х20) | 0(х21) | 1(х22) |
Например:
видно, что 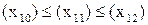 и
и 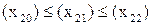 , то выполняется:
, то выполняется: 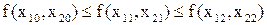
5) Если 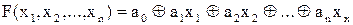 , где
, где 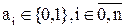 , то f(x1,x2,…,xn) – называется линейной логической функцией
, то f(x1,x2,…,xn) – называется линейной логической функцией
 2014-02-02
2014-02-02 508
508








