2014-02-02
395
Предположим, что зависимость выработки продукции на одного работника характеризуется следующим уравнением:
.
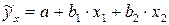На основании исходных данных составляем систему уравнений для определения коэффициентов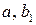 
и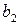 
.
;
; 
;
;
;
; 
;
.
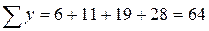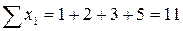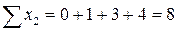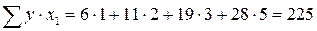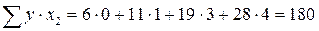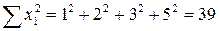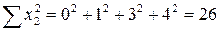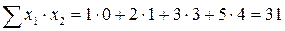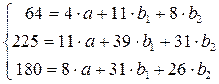
Решим эту систему по методу Крамера. Вычисляем определитель системы:
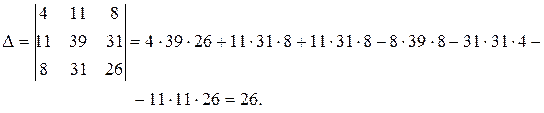
Аналогично вычисляем частные определители, заменяя соответствующий столбец столбцом свободных членов:
; 
; 
.
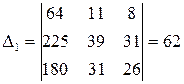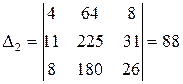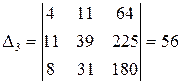Коэффициенты уравнения определяются по формулам:
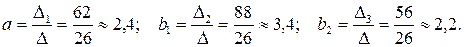
Таким образом, уравнение имеет вид:
.
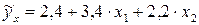Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
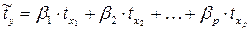, (4)
где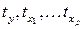 
- стандартизованные переменные: 
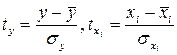, для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;
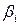- стандартизованные коэффициенты регрессии.
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида для определения стандартизованных коэффициентов регрессии.
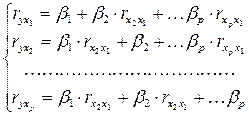. (5)
Следует отметить, что величины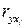 
и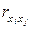 
называются парными коэффициентами корреляции и определяются по формулам
, 
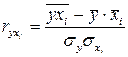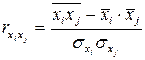. (6)
Решая систему (5) определяем стандартизованные коэффициенты регрессии. Сравнивая их друг с другом, можно ранжировать факторы по силе воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.
Пример. Получим для предыдущего примера уравнение регрессии в стандартизованном масштабе.
, 
, 
, 
;
;
.
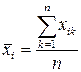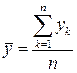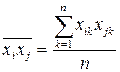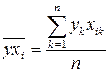
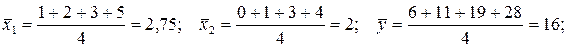
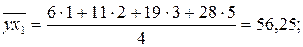
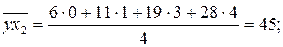
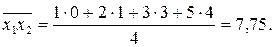
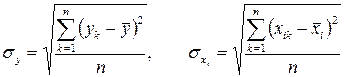
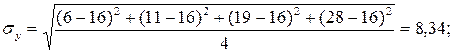
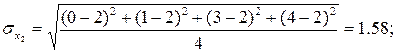
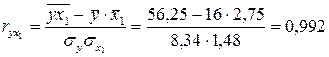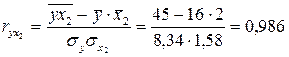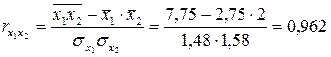Согласно (5) получаем систему нормальных уравнений в виде:
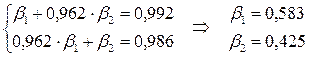
Окончательно получаем уравнение регрессии в стандартизованном масштабе в виде:
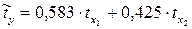
Используя формулы 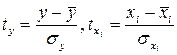можно вернуться к уравнению «чистой» регрессии:
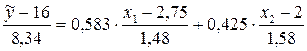
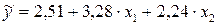
Сравнивая полученное уравнение с полученным ранее мы видим хорошее соответствие полученных разными способами результатов.
