Пример 1. Если у зн.ч. ряда n-й член стремится к 0 монотонно убывая, то ряд сх-ся, сумма ряда им

Теор Признак Лейбница

Если у зн.ч. ряда n-й член стремится к 0 монотонно убывая, то ряд сх-ся, сумма ряда им. знак 1го члена ряда и не превосх. его по модулю.

1 Пусть у зн.ч. ряда a1+a2-…-an+… lim |a_n|=0, |a1|³|a2|³|a3|³|an|=c_n тогда ряд запис. в виде с1-с2+с3-… (1), если a1³0 и –с1+с2-с3+… (2) если а1£0.

а1³0. Для частич. сумм с чёт. номерами n=2k имеем S_2k=c1-c2+c3-c4+…+c_2k-1-c_2k=

{(c1-c2)+(c3-c4)+…+ c_2k-1-c_2k (3)

{c1-(c2-c3)-(c4-c5)-…-c_2k (4). Т.к. с1³с2³…, то все скобки ³0, поэтому (3)Þ S_2k³0, посл. {S_2k} возрастает: S_2k+2 = S_2k+ (c_2k+1-c_2k+2)³ S_2k. (4)Þ S_2k£c1. Т.о. {S_2k} возрастает и ограничена сверхуÞ она имеет конеч. lim S, причём 0£ S_2k£с1Þ0£ S£с1.

Для посл-ти частич. сумм с неч. номерами n=2k имеем S_2k-1=c1-c2+…+c_2k-1=(c1-c2+…+c_2k-1-c_2k)+c_2k=S_2k+c_2kÞ

lim(k®¥) S_2k-1=(*по усл. lim(k®¥) c_2k=0*)= lim(k®¥) S_2k=S. Теперь покажем, что вся посл-ть {S_n} имеет предел S. Зададим e>0. Тогда lim(k®¥) S_2k=SÞ($n1): ("n=2k³n1)[|S_n-S|<e], а lim(k®¥) S_2k-1=SÞ($n2):("n=2k-1³n2)[|S_n-S|<e]. Возьмём n_e=max{n1,n2}. Тогда ("n> n_e)[|S_n-S|<e]. Это означ. Что lim S_n=S. Т.о. данный ряд сх-ся к сумме S, причём 0£S£c1Þ(*a1³0Þc1=a1*)Þ0£s£a1. Ан-но в случае a1£0 док-ся, что ряд сх-ся к S, причём –с1£S£0Þ(*а1£0Þ-с1=а1*)Þа1£S£0. Т.о. S и а1 имеют один знак, причём |S|£|a1| g

Опр. Знакочер. ряд удовл. условиям признака Лейбница наз-ся рядом лейбницевского типа. Любой остаток ряда лейб. типа есть т.ж. ряд лейб. типа, поэт верно следствие:

Следствие Об остатке ряда лейб. типа.

Любой n-й остаток ряда л.типа имеет знак 1-го члена этого остатка (т.е. члена a_n+1) и не превосх. его по модулю: |r_n|£|a_n+1|

1-1/2+1/3-1/4+…=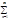(-1)^n-1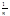- ряд лейб. типа, т.к. |an|=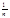®0 монотонно убывая Þ по признаку Лейбница ряд сх-ся. Ряд из модулей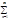 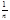- расх-ся (гарм. ряд) значит данный ряд сх-ся неабс.