Операции с множествами

Лекция 13.

Множества. Операции с множествами. Отображения множеств. Множество действительных чисел. Числовые множества. Функция. Область ее определения. Сложные и обратные функции. График функции. Основные элементарные функции. Предел функции в точке и на бесконечности. Свойства предела. Односторонние пределы. Предел числовой последовательности.

Замечание. Понятие множества, как и другие основополагающие понятия математики, вводится без определения.

1. Включение множества А в множество В 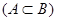. При этом каждый элемент множества А является элементом множества В, и множество А называется подмножеством множества В. В частности, А=В, если все элементы множества А принадлежат множеству В и наоборот.
2. Объединение множеств А и В - множество элементов, каждый из которых принадлежит хотя бы одному из множеств А и В.
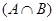3. Пересечение множеств А и В - множество всех элементов, принадлежащих одновременно А и В.
4. Разность множеств А и В (А\В) – множество элементов множества А, не принадлежащих множеству В.

Определение 13.1. Множество, не содержащее ни одного элемента, называется пустым множеством.

Определение 13.2. Пусть заданы непустые множества Х и Y. Соответствие, при котором каждому элементу множества Х соответствует некоторый элемент множества Y, называется отображением Х на Y.