2014-02-02
647
В соответствии с законом Ампера на активные стороны секции якоря, находящейся в данный момент под током I, действует пара сил F, создающая вращающий момент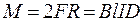 
(рис. 2.9).
Рис. 2.9
Пара сил на рис. 2.9 вращает якорь против часовой стрелки. Направление тока в секциях ОЯ меняется на противоположное каждый раз при повороте якоря на 180 град. За счет этого направление вращающего момента во времени не изменяется.
Таким образом, если в генераторах ЩКУ выполняет роль механического выпрямителя, то в двигателях постоянного тока он выполняет роль механического инвертора, изменяющего направление тока в секциях ОЯ.
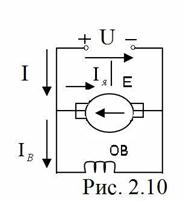
На рис. 2.10 показана схема двигателя постоянного тока параллельного возбуждения, для которой справедливы следующие уравнения:
– первое уравнение Кирхгофа
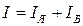, (2.11)
где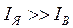 
;
Уравнение электрического баланса цепи якоря
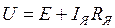, (2.12)
где E=CenФ – ЭДС двигателя или противоЭДС.
В номинальном режиме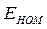 
≈ (0,9
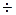0,95)U.
При пуске двигателя постоянного тока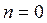 
и противоЭДС Е = 0. При этих условиях
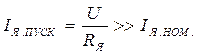
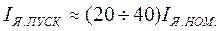
Для ограничения пускового тока в цепь якоря на время пуска последовательно включают добавочный резистор, ограничивающий ток якоря до безопасного значения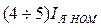
, т.е.
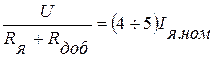
По мере разгона двигателя противоЭДС увеличивается и в соответствии с уравнением (2.12) ток якоря будет уменьшаться до значения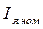 
. При этом резистор 
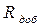закорачивается.
Вращающий момент М двигателя постоянного тока определяется из выражения
,
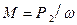где Р2 – полезная мощность на валу двигателя;
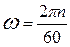–угловая скорость вала двигателя, рад/c (2.13)
n – частота вращения двигателя, об/мин.
Если пренебречь потерями холостого хода в магнитопроводе и подшипниках, то из энергетического баланса двигателя параллельного возбуждения следует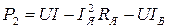 
. С учетом выражений (2.11) и (2.12) получим
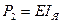. (2.14)
Подставляя (2.14) и (2.13) в выражение для момента, найдем
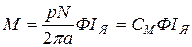, (2.15)
где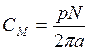 
- константа по моменту двигателя.
Механическая характеристика двигателя – это зависимость частоты вращения от момента на валу, т.е.
.
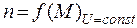Для двигателя параллельного или независимого возбуждения с добавочным сопротивлением в цепи якоря справедливо уравнение
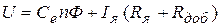. (2.16)
Откуда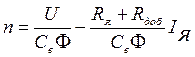 
(2.17)
Последнее выражение часто называют скоростной характеристикой двигателя. Подставляя в него ток из уравнения (2.15), получим аналитическое выражение механической характеристики
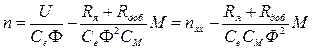, (2.18)
где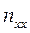 
-частота вращения якоря при холостом ходе.
На практике для двигателей независимого и параллельного возбуждения пользуются более удобной формулой для механической характеристики, в которую входят параметры, определяемые по данным технического паспорта. В указанных двигателях поток Ф остается практически постоянным, поэтому выражение (2.18) для электромагнитного момента можно записать
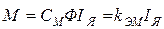, (2.19)
где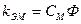 
– электромагнитный коэффициент двигателя.
Тогда выражение для противо-ЭДС двигателя с учетом уравнений (2.8), (2.13) и (2.15) примет вид:
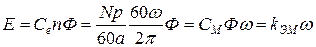. (2.20)
С учетом выражения (2.20) уравнение (2.12) можно записать как
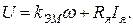(2.21)
Подставляя в уравнение (2.21) выражение для тока из (2.19), получим
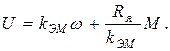(2.22)
Из уравнения (2.22) получим искомое выражение для механической характеристики
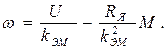(2.23)
Из уравнения (2.21) для номинальных значений параметров двигателя, приводимых в справочниках, получим
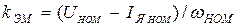. (2.24)
