2014-02-02
1179
При пуске двигателя напряжение U на якоре изменяется скачком. Известно, что любой переходный процесс можно описать дифференциальным уравнением, которое для цепи якоря имеет вид
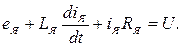(2.26)
При t = 0
U = 0, при t =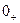
U=const.
Для двигателя независимого (параллельного) возбуждения электромагнитный момент равен
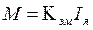. (2.27) I
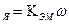, (2.28) где
.
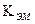
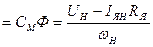При холостом ходе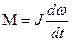 
, (2.29)
где J - момент инерции якоря. Тогда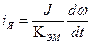 
. (2.30)
Подставляя (2.28) и (2.30) в (2.26), получим после некоторых преобразований
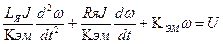, (2.31)
. (2.32)
где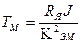 
- электромеханическая постоянная времени двигателя,
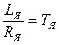- электромагнитная постоянная времени якоря двигателя, 
.
Решение уравнения (2.32) имеет вид
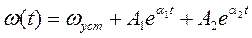, где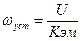 
.
Окончательно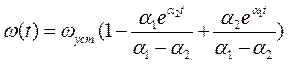 
.
Возможный характер изменения угловой скорости двигателя при пуске изображен на рисунке 2.12.
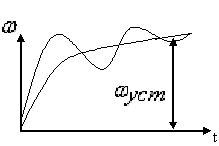
Рис. 2.12
Перейдем к операторной форме дифференциального уравнения (2.32)
, (2.33),
из которого получим передаточную функцию ДПТ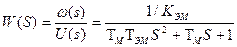 
, где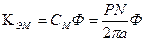 
, 
.
Корни характеристического уравнения - 
. (2.34)
Если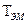 
→ 0, то из (2.33) 
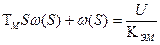. (2.35).
Тогда 
. (2.36)
Так как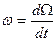 
и 
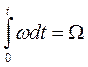, то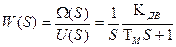 
. (2.37)
Если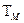 
пренебречь, т.е. считать, что время переходных процессов разгона и торможения двигателя много меньше времени отработки задания, т.е. 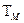0, то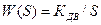 
. Следовательно в этом случае двигатель, относительно угла поворота, является интегрирующим звеном системы управления.
|
|
|
