Логико - информационные модели

Результаты обследования управленческих работ и потоков информации для удобства описания и полноты анализа можно представить в виде так называемых логико-информационных моделей. Они позволяют символически выразить технологию подготовки данных и маршруты движения документов, алгоритмы формирования показателей, а также взаимосвязь между всеми подразделениями предприятия и внешней среды. Основное назначение логико-информационной модели в том, что она характеризует существующие потоки информации, необходимые для анализа документооборота и проектирования системы обработки данных, и их оптимизацию, а также выбора комплекса технических средств.

В настоящее время применяется ряд информационных моделей: матричные, в виде "шахматной" таблицы, блок-схема, сетевые графики, математические модели анализа информационных потоков.

Матричные информационные модели разработаны в ЦЭМИ АН СССР. Они позволяют в единой форме отразить связи между подразделениями предприятия и процессы выработки новых сведений. Это модель выявленных потоков информации системы или любого ее подразделения. Она выражает количественно все характеристики подразделения. Матричные информационные модели отличаются степенью детализации (показатели, задачи, документы) и уровнем, для которого строятся (подразделения, предприятие, объединение).

Наибольшее распространение получили матричные информационные модели типа А-модель в виде шахматной таблицы и типа Б- матричная модель документообразования и документооборота.

Логико-информационная модель в виде шахматной таблицы.

В модели типа А по подлежащему таблицы приводятся функциональные подсистемы с расчленением на задачи, реализующие те или иные функции. В сказуемом таблицы приводится перечень структурных подразделений управленческого аппарата предприятия. Каждый элемент таблицы, лежащий на пересечении строк и столбцов (задача и ее исполнитель), делится на 3 части: вверху слева указываются шифры входной переменной информации, вверху справа - шифры нормативной, внизу - выходной. Эта модель называется шахматной.

Общий вид матричной логико-информационной модели в виде шахматной таблицы(тип А) можно представить так (рис 3.3.1):

Функциональные подсистемы в бухгалтерском учете обычно состоят из большого количества задач, поэтому модель можно ограничить рамками одной подсистемы. На рис 3.3.1 показана схема модели на примере трех подразделений П₁, П₂, П₃ и трех задач.

a_ij, b_km, g_tf - потоки информации.

Подразд. Задачи	П1	П2	П 3
ЗАДАЧА 1	a11 b11 g11	a12 g11 g12
ЗАДАЧА 2	a11 b11 g22		a11 g21 g23
ЗАДАЧА 3		g22 g23 g13	g13 g21 g23

Рис 3.3.1 Шахматная логико-информационная модель

Поток информации, являясь выходным относительно одной задачи или исполнителя, будет входным относительно другой задачи или исполнителя. Этот факт отражается в одинаковом коде (наименовании) потоков выходной информации из одной задачи и входной для другой задачи. Для подразделения, разрабатывающего нормативы, шифры этих нормативов - выходная информация, а для подразделения, использующего эти нормативы - нормативная входная информация. Таким образом, фиксируемая связь структурных подразделений позволяет при рассмотрении строк этой таблицы выявить структурные подразделения, принимающие участие в решении задачи, а при рассмотрении столбцов таблицы можно перечислить задачи, входящие в компетенцию структурного подразделения.

Для подготовки информационной основы модели, сведения о потоках информации можно отобразить в таблице

Наименование задачи	Шифр задачи	Входная нормативная информация	Входная переменная информация	Выходная нормативная информация	Выходная переменная информация	Код подраделения

Матричная логико-информационная модель.

В модели типа Б отражаются связи для каждого структурного подразделения предприятия в резерве показателей и документов. Общий вид информационной модели типа Б можно представить следующей таблицей, которая состоит из 4 частей-квадрантов

(рис 3.3.2):

II кв.

I кв. P1 Pk

Док Док

D1

DI

DJ

P1

PI

Pk

a11

a12

ai1

ai2

aj1

aj2

…

D1

a11

X

a12

X

DI …

ai1

X

ai2

X

DJ

aj1

X

aj2

X

…

X

Dm

am1

am2

Dn

an1

an2

III КВ. IV КВ.

Рис 3.3.2 Схема документообразования

В первом квадранте матрицы отражаются все документы и показатели в обследуемом подразделении.

Квадрант П отражает выход разработанных в данном подразделении документов и показателей по потребителям.

Квадрант Ш отражает применяемость поступающих показателей и количество входящих показателей для формирования показателя квадранта I или их переписку в новый документ.

Квадрант IV характеризует передачу данным подразделениям документов, поступающих другим подразделениям. Квадранты I и IV совместно показывают процесс создания документов и выход их в другие подразделения; I и II отражают процесс формирования документов и показателей в данном подразделении; II и IV отражают выход всех документов и показателей, которые создаются в данном подразделении или поступают из других подразделений; III и IV вместе взятые, отражают использование или контроль, или простую переписку документов и показателей, необходимых для деятельности данного подразделения. Если поступивший документ или показатель не используется в данном подразделении или передается другим подразделениям, то делается специальная отметка в соответствующем квадранте.

Если показатель строки участвует в образовании показателя, обозначенного в столбце, то на пересечении соответствующей строки и столбца проставляется 1. Аналогично заполняется и поступление документа в подразделение.

- Для построения матричных моделей используются следующие исходные данные, получаемые в результате обследования предприятия:

- перечень наименований документов, поступающих в подразделение;

- перечень наименований документов, разрабатываемых в данном подразделении;

- перечень всех выходящих документов из подразделения с указанием адреса;

- наименования показателей в конкретном документе, поступающем в подразделение.

Логико-информационные модели в виде сетевых графиков

Для наиболее важных и ответственных участков управления (например, планово-экономическая служба) циркулирование потомков информации может быть представлено в виде сетевой модели. Здесь "событие" означает формирование документа или принятие решение, "работа" - поток информации. Модель наглядно иллюстрирует излишнюю информацию. В этом случае потоки информации не входят ни в одно событие. Дублируемая информация изображается следующим образом: одни и те же потоки информации входят в одно событие, однако их источниками являются разные события.

В результате обследования можно выработать предложения по условиям ввода системы в эксплуатацию, рекомендации по совершенствованию документооборота, по централизации и децентрализации системы обработки данных. Вид модели следующий: (Рис 3.3.3)

Рис 3.3.3 Сетевая логико-информационная модель

Математические модели анализа информационных потоков

Для создания анализа информационных потоков, установления групп очередности обработки документов широко применяются математические модели, построенные с использованием теории графов. Эти модели предполагают построение обобщенной матрицы смежности и обобщенного информационные графа.

Прежде чем перейти к построению информационной матрицы смежности, рассмотрим некоторые основные понятия из теории графов.

ГРАФ - множество V вершин и набор Е неупорядоченных и упорядоченных вершин. Обозначается Граф через G(V,E). Неупорядоченная пара вершин называется ребром, упорядоченная пара - дугой. Граф, содержащий только ребра, называется неориентированным; содержащий только дуги - ориентированным. Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующим вершинам, которые соединены линиями, соответствующими ребрам или направленным дугам. Вершины, соединенные ребром или дугой, называются смежными. Говорят, что ребро или дуга (u, v) начинается в вершине u и кончается в вершине v. В ориентированном графе G для каждой вершины u_i и v_J можно определить полустепень исхода и полустепень захода как количества дуг, выходящих из этой вершины и входящих в нее соответственно. Каждый обобщенный граф можно разбивать на простые(структурные) графы. Если в графе для вершин u_i (i>1) полустепень исхода>0 и для вершин v_J (j=1) полустепень исхода=0, то такой граф будем называть структурным.

Объединением(обобщением) графов G₁ и G₂ называется граф

G= G₁UG₂ с множеством вершин V= V₁UV₂ и множеством ребер

E= E₁UE₂.

Существуют различные способы задания графа. Пусть u₁, u₂,…, u_n – вершины графа G(V,E), е₁, е₂,…, е_m – его ребра.

Матрицей смежности, соответствующей графу G, называется матрица A=||a_ij||, у которой элемент a_ij равен числу ребер(дуг), соединяющих вершины u_i и u_j (идущих от u_i к u_j), и a_ij=0, еслисоответствующие вершины не смежны.

Теория графов относится к области дискретной математики, особенностью которой является геометрический подход к изучению объектов.

Следуя основным определениям теории графов, можем сказать, что задача является структурным графом, а комплекс задач заданной предметной области объединяется в обобщенный граф.

Порядок построения математической модели анализа информационных потоков следующий:

1. На основании изучения состава документов устанавливается связь между входными и выходными документами.

2. На основе установленных взаимосвязей строят структурные графы.

3. Описывают аналитически каждый граф с помощью описания множества вершин и отображений.

4. Строят обобщенное множество вершин и отображений.

5. Строят обобщенную матрицу смежности и определяют очереди обработки документов.

6. Дают рисунок обобщенного информационного графа.

7. Выписывают входные, промежуточные и выходные документы.

Построение математической модели анализа рассмотрим на условном примере.Пусть решаются четыре задачи, т.е. установлены четыре взаимосвязи между документами:

Задача1. Документ D3 формируется на основании документов D1 и D2.

Задача2. Документ D6 формируется на основании документов D3,D4 и D5.

Задача3. Документ D7 формируется на основании документов D4 и D26.

Задача4. Документ D8 формируется на основании документов D3 и D27

Построим модель, следуя установленному порядку.

1) Составим структурные графы

Граф 1Граф 2Граф 3Граф 4 D1 D2 D3 D4 D5 D4 D6 D3 D 7

D3 D6 D7 D8

2) Опишем каждый граф аналитически.

Граф 1:

Множество вершин:

V1={D1, D2, D3 }

Множество отображений:

E1: Г_1D1=Г_1D2={D3}

(В графе 1 документ D1, равно как документ D2 участвуют в формировании документа D3).

Граф 2:

Множество вершин:

V2={D3, D4, D5,D6}

Множество отображений:

E2: Г_2D3=Г_2D4= Г_2D5={D6}

Граф 3:

Множество вершин:

V3={ D4,D6,D7}

Множество отображений:

E3: Г_3D4=Г_3D6 ={D7}

Граф 4:

Множество вершин:

V4={ D3,D7,D8}

Множество отображений:

E4: Г_4D3=Г_4D7 ={D8}

Строим обобщенное множество

Вершин: V1 U V2 U V3 U V4= ={D1, D2, D3 }U{D3, D4, D5,D6}U {D4,D6,D7}U{ D3,D7,D8}

Отображений: E1 U E2 U E3 U E4

Г_1D1={D3}

Г_1D2={D3}

Г_2D3=Г_4D2={D6,D8}

Г_2D4=Г_3D3={D6,D7}

Г_2D5 ={D6}

Г_3D6 ={D7}

Г_4D7 ={D8}

Строим обобщенную матрицу смежности. Это матрица, по столбцам и строкам которой записан перечень обрабатываемых документов. Для каждого элемента a_ij проставляем 1 или 0 (по количеству ребер, соединяющих вершины)

	D1	D2	D3	D4	D5	D6	D7	D8
D1
D2
D3
D4
D5
D6
D7
D8

Определяем очереди обработки. В матрице выделяем столбцы, у которых a_ij=0 («пустые» столбцы). Соответственно выделяем строки с такими же кодами. Это документы нулевой очереди обработки. (D1,D2,D4,D5) Строим усеченную матрицу, используя не выделенные элементы.

	D3	D6	D7	D8
D3
D6
D7
D8

Вновь отсекаем «пустые» столбцы. Это документы первой очереди обработки (D3). Продолжаем этот процесс до тех пор, пока ни получим нулевую матрицу.

	D6	D7	D8
D6
D7
D8

D6- документ второй очереди обработки.

	D7	D8
D7
D8

D7-документ третьей очереди обработки.

D8-документ четвертой очереди обработки

Строим обобщенный информационный граф. На каждом уровне его располагают вершины, соответствующие выделенным очередням обработки докумнтов. Вершины соединяют дугами.

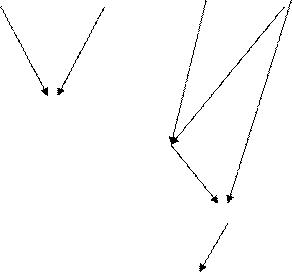D1 D2 D5 D4 0 очередь

D3 1 очередь

D6 2 очередь

D7 3 очередь

D8 4 очередь

Рис 3.3.4. Обобщенный информационный граф

Вершины, из которых только выходят дуги, будут соответствовать входным документам. (D1,D2,D4,D5).

Вершины, из которых и выходят дуги и входят в них, будут соответствовать промежуточным (производным) документам. (D3,D6,D7)

Вершины, в которые только выходят дуги, будут соответствовать выходным документам. (D8)