Алгоритм Левенберга-Марквардта

В данном алгоритме используется квадратичное приближение целевой функции E(w), представленной формулой (2.3) в окрестности полученного решения .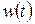

Для достижения минимуму целевой функции требуется, чтобы 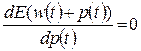. При выполнении соответствующего дифференцирования можно получить условие оптимальности в виде:

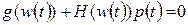, откуда следует

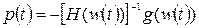(3.41)

Формула (3.41) однозначно указывает направление 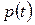, которое гарантирует достижение минимального для данного шага значения целевой функции. Из него следует, что для определения этого направления необходимо в каждом цикле вычислять значение градиента g и гессиана H в точке последнего решения .

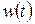Формула (3.41) представляет собой основу ньютоновского алгоритма оптимизации и является чисто теоретическим выражением, поскольку ее применение требует положительной определенности гессиана на каждом шаге, что практически не осуществимо. Поэтому в реальных алгоритмах вместо точно определенного гессиана 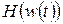используется его приближение 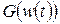, которое в алгоритме Левенберга-Марквардта рассчитывается на основе содержащейся в градиенте информации с учётом некоторого регуляризационного фактора [4].

Для описания данного метода представим целевую функцию в виде:

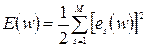, (3.42)

где 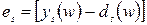. При использовании обозначений

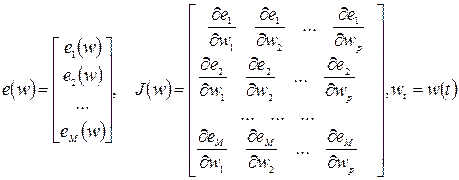. (3.43)

Вектор градиента и аппроксимированная матрица гессиана, соответствующие целевой функции (2.30) на 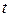-ом шаге алгоритма, определяются в виде:

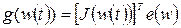, (3.44)

, (3.45)

где 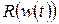обозначены компоненты гессиана 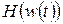, содержащие высшие производные относительно 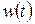. Аппроксимация 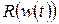осуществляется с помощью регуляризационного фактора 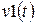, в котором переменная 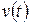называется параметром Левенберга-Марквардта и является скалярной величиной, изменяющейся в процессе обучения. Таким образом:

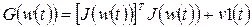. (3.46)

В начале процесса обучения, когда текущее решение 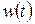далеко от искомого решения, следует использовать значение параметра 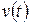намного превышающее 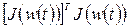. В этом случае гессиан фактически заменяется регуляризационным фактором:

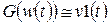, (3.47)

а направление минимизации выбирается по методу наискорейшего спуска:

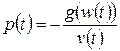. ё (3.48)

По мере приближения к искомому решению величина параметра 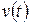понижается и первое слагаемое в формуле (2.34) начинает играть более важную роль. Таким образом, на эффективность алгоритма влияет правильный выбор величины 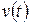. В методике, предложенной Д.Марквардтом, значение 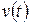изменяется по следующей схеме:

;

;

,

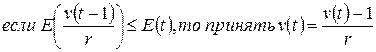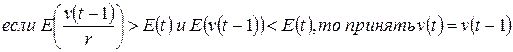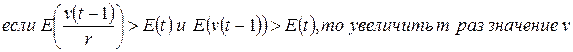
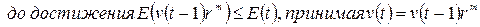где 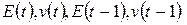обозначают значения целевой функции и параметр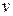а на 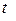-ом и 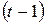-ом шагах алгоритма, а 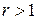- обозначает коэффициент уменьшения .

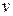Такая процедура изменения 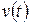применяется до момента, когда коэффициент верности отображения, рассчитываемый по формуле

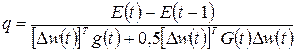, (3.49)

достигнет значения, близкого к единице. При этом квадратичная аппроксимация целевой функции имеет высокую степень совпадения с истинными значениями, следовательно, регуляризационный фактор в формуле (2.34) может быть приравнен нулю, а процесс определения гессиана сводится к аппроксимации первого порядка, при этом алгоритм Левенберга-Марквардта превращается в алгоритм Гаусса-Ньютона, имеющему квадратичную сходимость.